A dipole antenna can be visualized as a single port device. Port connects the source to the antenna. At this port, consider the following:
VSWR => Voltage Standing Wave Ratio
\(Γ\) => Reflection coefficient
\(S_{11} = \frac{\text{reflected wave (from the port)}}{\text{incident wave (from the source)}} = Γ\)
we know,
$$ VSWR = \frac{1+|Γ|}{1-|Γ|} ≥ 1$$
Case-1: \(VSWR = 1\)
$$ \frac{1+|Γ|}{1-|Γ|} =1 $$
$$ ∴ 1+|Γ| = 1-|Γ|$$
$$ ∴ |Γ|=0 $$
Which implies zero reflections and is the ideal case.
in dB,$$ S_{11} (dB) = 20log_{10}(|Γ|) = 20log_{10}(0) = -∞$$
This is practically not possible.
Case-2: \(VSWR = 2\)
$$ \frac{1+|Γ|}{1-|Γ|} =2 $$
$$ ∴ 1+|Γ| = 2-2|Γ|$$
$$ ∴ 3|Γ|=1 $$
$$ ∴ |Γ|=1/3 $$
This implies \(2/3^{rd}\) of the total wave is transmitted and the rest \(1/3^{rd}\) is reflected.
in dB, $$ S_{11} (dB) = 20log_{10}(|Γ|) = 20log_{10}(1/3) = -9.54 \text{ dB} $$
$$ ∴ S_{11} (dB) ≈ -10 \text{ dB} $$
This case is widely considered for calculating the impedance bandwidth of an antenna.
The difference between highest and lowest frequencies at points where the \(-10 \text{ dB}\) line cuts the \(S_{11}\) curve is called the impedance bandwidth.
Case-3: \(VSWR = 3\)
$$ \frac{1+|Γ|}{1-|Γ|} =3 $$
$$ ∴ 1+|Γ| = 3-3|Γ|$$
$$ ∴ 4|Γ|=2 $$
$$ ∴ |Γ|=1/2 $$
This implies half of the total wave is transmitted and the rest half is reflected.
in dB, $$ S_{11} (dB) = 20log_{10}(|Γ|) = 20log_{10}(1/2) $$
$$ ∴ S_{11} (dB) = -6.02\text{ dB} > -10 \text{ dB} $$
More reflection occurs in this case. Hence the above case is preferred.
Case-4: \(VSWR = 4\)
$$ \frac{1+|Γ|}{1-|Γ|} =4 $$
$$ ∴ 1+|Γ| = 4-4|Γ|$$
$$ ∴ 5|Γ|=3 $$
$$ ∴ |Γ|=3/5 $$
This implies \(2/5^{th}\) of the total wave is transmitted and the rest \(3/5^{th}\) is reflected.
in dB, $$ S_{11} (dB) = 20log_{10}(|Γ|) = 20log_{10}(3/5) $$
$$ ∴ S_{11} (dB) = -4.437\text{ dB} > -10 \text{ dB} $$
More reflection occurs in this case too. Hence the case-2 is preferred.
Finally, the bandwidth is calculated as \((f_2 - f_1)\) as shown below:
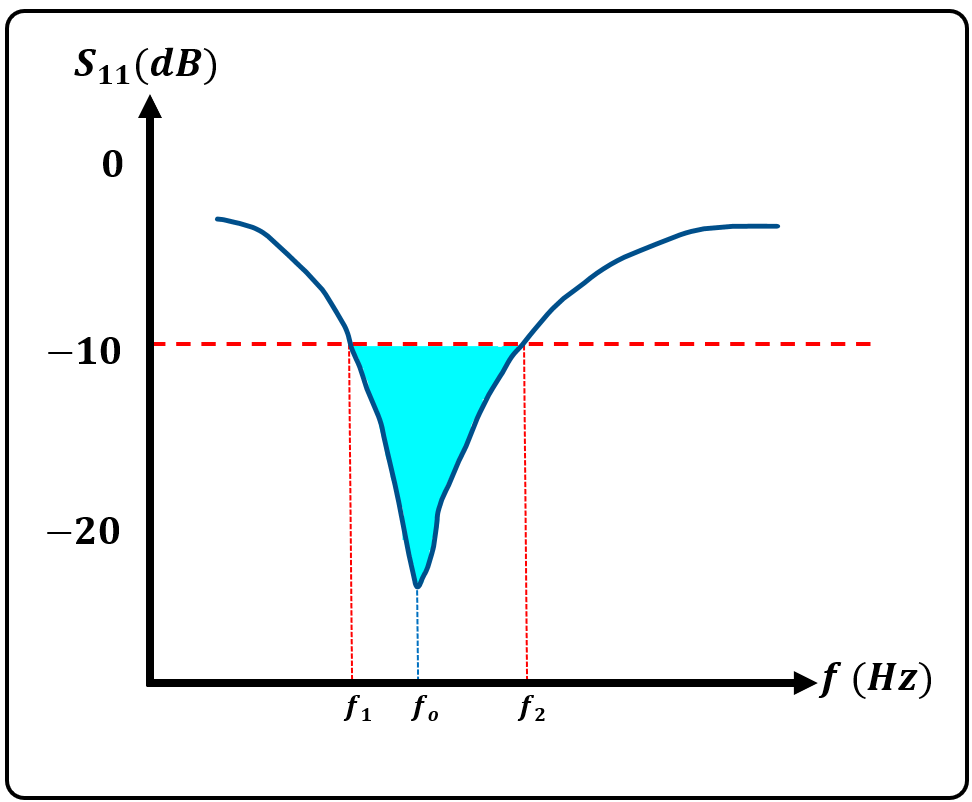
\(\text{Impedance Bandwidth } = f_2-f_1\)
\(f_o \text{ is the resonant frequency}\)
Shaded region specifies the range of frequencies for which the antenna radiates.