Consider an infinitesimal dipole element (also known as Hertz Dipole), placed at the origin of a coordinate system.

Considering spherical coordinates, the different components of E (Electric Field vector) and H (Magnetic Field vector) can be given by the equations below.

Electric Field components -

$$ E_r = \frac{\eta I_odlcos\theta}{2\pi r^2}\left[1-j\frac{1}{kr}\right] e^{(-jkr)}$$

$$ E_\theta = j \frac{\eta k I_odlsin\theta}{4\pi r}\left[1-j\frac{1}{kr}-\frac{1}{(kr)^2}\right] e^{(-jkr)}$$

$$ E_{\phi} = 0 $$

Magnetic Field components -

$$ H_r = 0 $$

$$ H_{\theta} = 0 $$

$$ H_{\phi} = \frac{I_odlsin\theta}{4\pi}\left[\frac{jk}{r}+\frac{1}{r^2}\right] e^{(-jkr)}$$

where

• \(E_r, E_{\theta}, E_{\phi} \) are the radial, polar and azimuth components of Electric Field respectively
• \(H_r, H_{\theta}, H_{\phi} \) are the radial, polar and azimuth components of Magnetic Field respectively
• \( \eta \) is the intrinsic impedance
• \( I_o \) is the magnitude of current
• \( dl \) is a small length element of the dipole
• \( r \) is the radial distance of an observation point from the origin
• \( \theta \) is the polar angle
• \( \phi \) is the azimuth angle
• \( k = \frac{2\pi}{\lambda} \) is the wave number

---

Wave impedance for a particular value of wavelength can be found by the taking the ratio of polar component of E and azimuth component of H which is as follows:

$$ \text{Wave impedance } (Z) = \frac{E_{\theta}}{H_{\phi}} $$

$$ \therefore Z = \frac{j \frac{\eta k I_odlsin\theta}{4\pi r}\left[1-j\frac{1}{kr}-\frac{1}{(kr)^2}\right] e^{(-jkr)}}{\frac{I_odlsin\theta}{4\pi}\left[\frac{jk}{r}+\frac{1}{r^2}\right] e^{(-jkr)}}$$

$$ \therefore Z = \eta \frac{\left(1-j\frac{1}{kr}-\frac{1}{(kr)^2}\right)}{\left(1-j\frac{1}{kr}\right)} $$

After plotting the magnitude and phase of \(Z\), the following graph is obtained (Software used: MATLAB R2023a) -

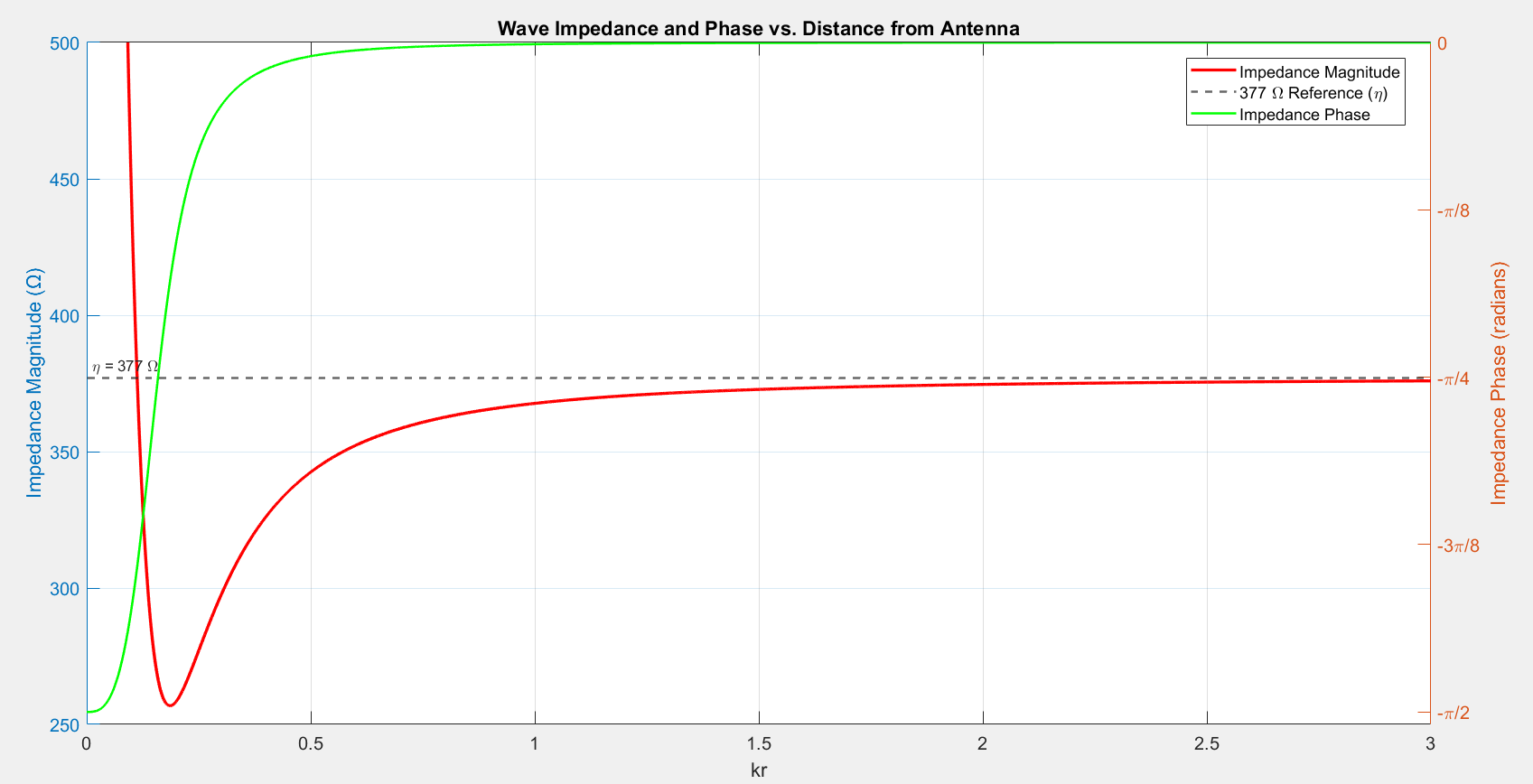
(The frequency is taken to be 300 MHz and the corresponding wavelength is equal to 1m)

Observations:

• In the near field (\(kr<< 1\), regions very close to the antenna), the field is predominantly capacitive and the phase angle is close to -90^o. In the near field (\(kr< 1\), regions close to the antenna), the inductive component of the field starts becoming appreciable and the phase angle takes a value between -90^o and 0^o.
• In the intermediate field \((kr>1)\), the wave impedance starts approaching the intrinsic impedance of free space and the reactive components of the fields starts getting convetred into radiative components. The phase starts approaching zero.
• In the far field region (\(kr>>1\)), the fields stabilize into a radiative form, where the wave impedance approaches the intrinsic impedance of free space \(\eta = 377 \text{ } \Omega\) Here, the electric and magnetic fields are in phase, and the impedance is real, indicating a propagating wave in free space.