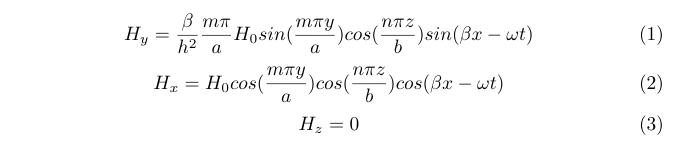
Modal fields inside a rectangular waveguide can be readily obtained by solving the standard lossless wave equations for E and H(∇2E+k2E=0, similarly for H), coupled with Faraday's law(∇XE=-jωH). We first note that rectangular waveguides can support either transverse-electric(TE) or transverse-magnetic(TM)modes(or hybrid modes) but not TEM modes. Here we consider a specific mode, namely TE10.
As explained above, we solve the wave equation along with Faraday's law, and apply the boundary conditions - electric field must be zero at each face of the waveguide(since we assume perfect conductors). Coupling this with the separation of variables method, we can find all field compenents.
Here we focus on finding the components of the magnetic field (H), as they are responsible for introducing currents on the surfaces of the waveguide. For TEmn mode, we have, in time domain:
Note: Here we are using the convention that wave propagation is in x-direction, and equations are written accordingly.
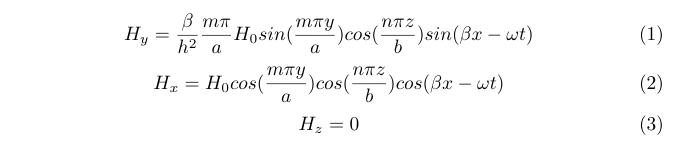
where a,b are the dimensions of the waveguide,H0 is the wave amplitude(assume unity) and h2=(mπ/a)2+(nπ/b)2
We find the surface currents at each face using the relation Js=anX(H1-H2), where an is the unit outward normal. Since fields outside the waveguide are zero, H2=0. This gives us an expression for the surface currents: (Note that the waveguide dimensions are normalized, and have been assumed equal. Further, put β=1 for simplicity)
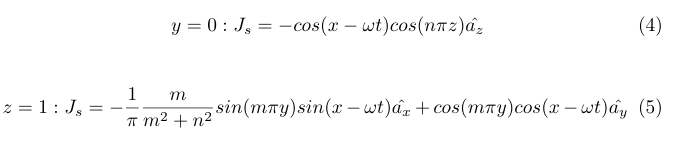
We plot these surface currents for m=1 and n=0, on the y=0 and z=1 faces. The y=1 and z=0 faces' surface currents are simply a mirror image of their counterparts.
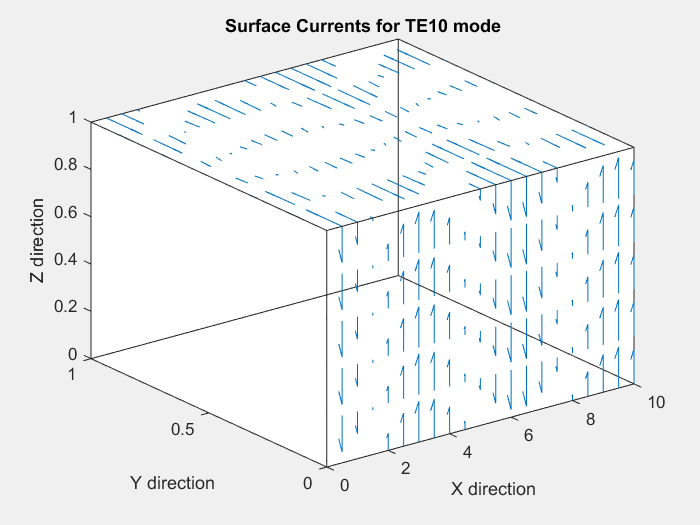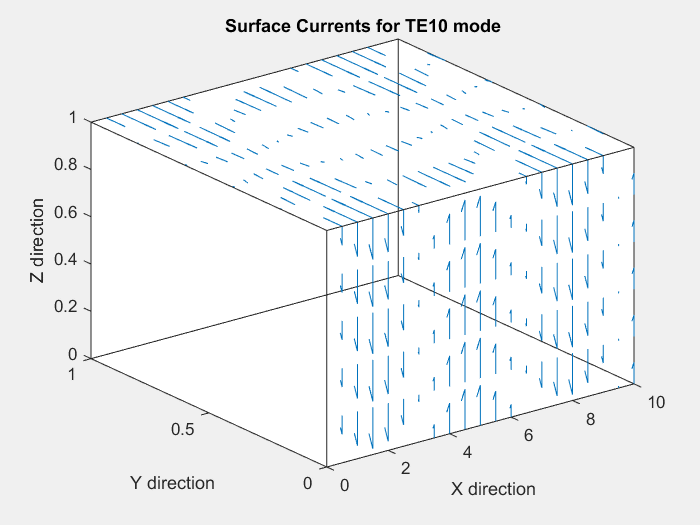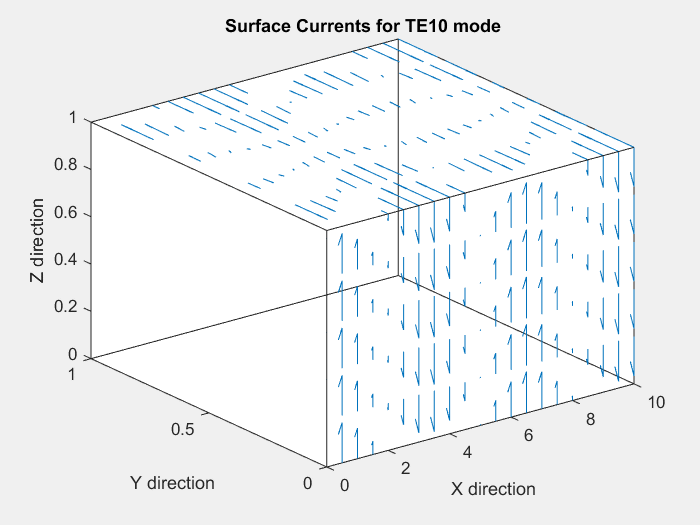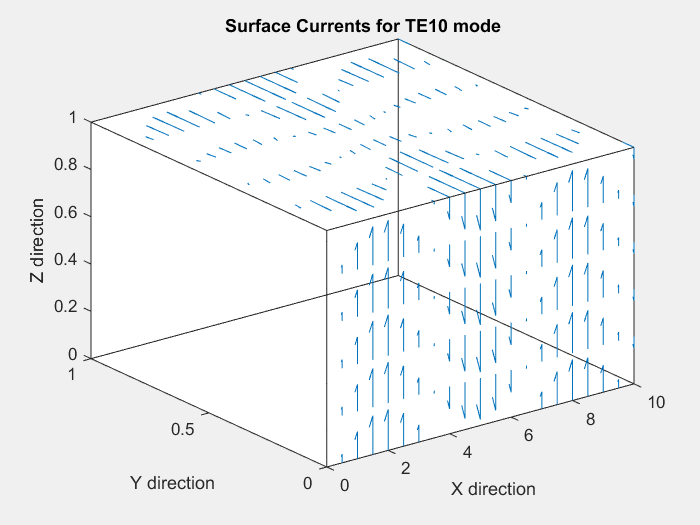
We observe that for the y=0 face, since n=0, the surface currents are always vertical, and vary in magnitude sinusoidally along the direction of propagation(x-direction).
For the z=1 face, we observe 2-D standing wave patterns in x and y that vary with time, as expected