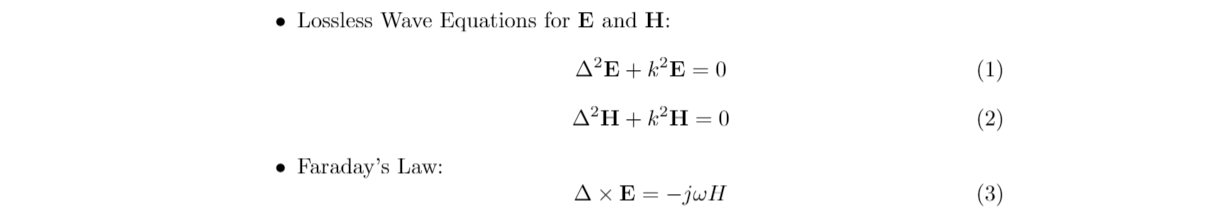
Waveguides are used to transfer electromagnetic power efficiently from one point in space to another. The most common waveguides have rectangular cross-sections and so are well suited for the exploration of electrodynamic fields that depend on three dimensions.
The expressions for Electric and Magnetic fields inside a rectangular waveguide are obtained using Faraday's Law and Lossless Wave Equations for the respective E and H fields, as shown below:
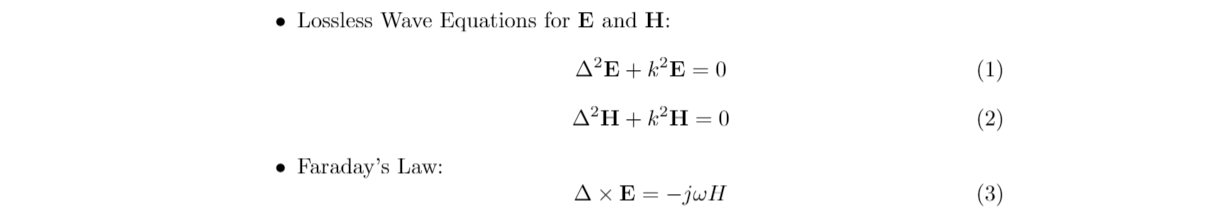
Rectangular waveguides support Transverse Electric (TE) and Transverse Magnetic (TM) modes and are incapable of supporting TEM modes.
According to the boundary conditions, the Electric field must be zero at each face of the waveguide (as the material of the waveguide is assumed to be a perfect conductor). Using these boundary conditions, along with separation of variables, we derive all field components. For the visualization of surface currents, we only need the Magnetic Field components. This is because:
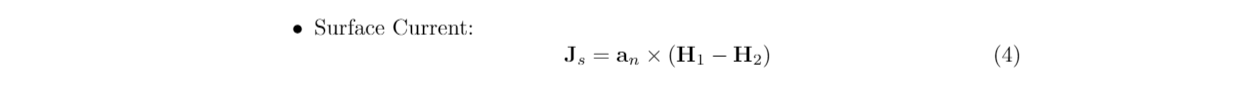
So using (1),(2) and (3) and applying the boundary conditions, we get the following Magnetic Field Intensity Expressions (for TE mn case) :
Note: The direction of wave propogation has assumed to be in the x-direction.
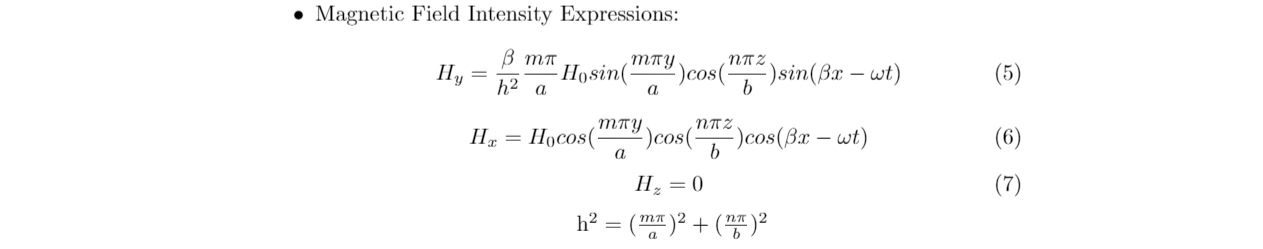
where a,b are the dimensions of the waveguide, H0 is the wave amplitude (assumed to be unity).
We find the surface currents at faces y=0 and z=1 using (4). Since fields outside the waveguide are zero, H2=0. This gives us an expression for the surface currents. For m=3 and n=2, these reduce to:
Note: The waveguide dimensions are normalized, and have been assumed equal. For simplicity, put β=1.
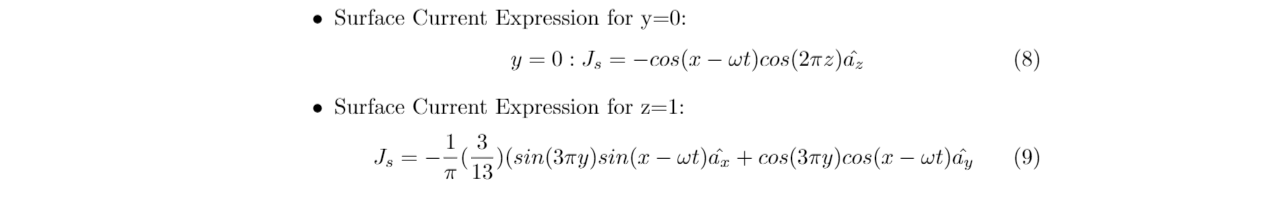
The surface currents varying with time have been shown in the figure below:
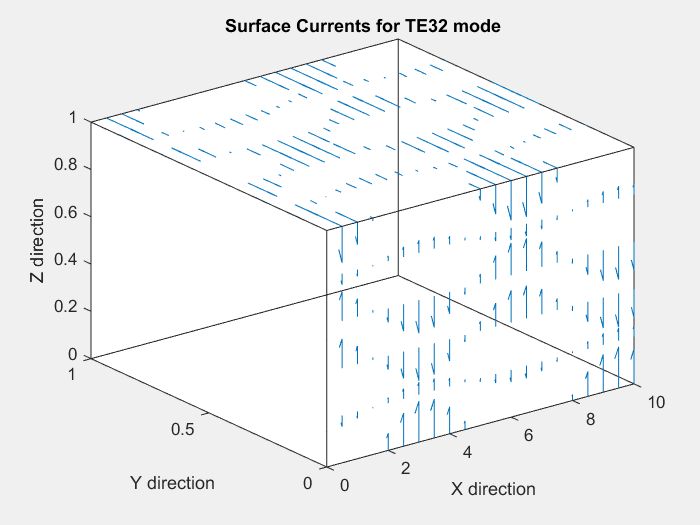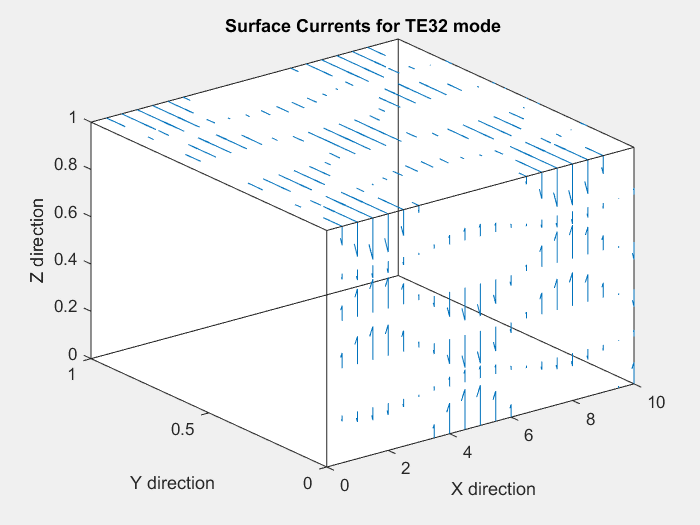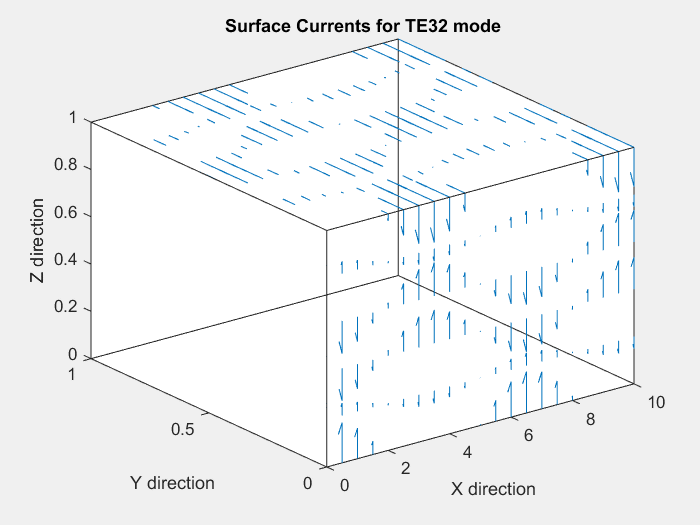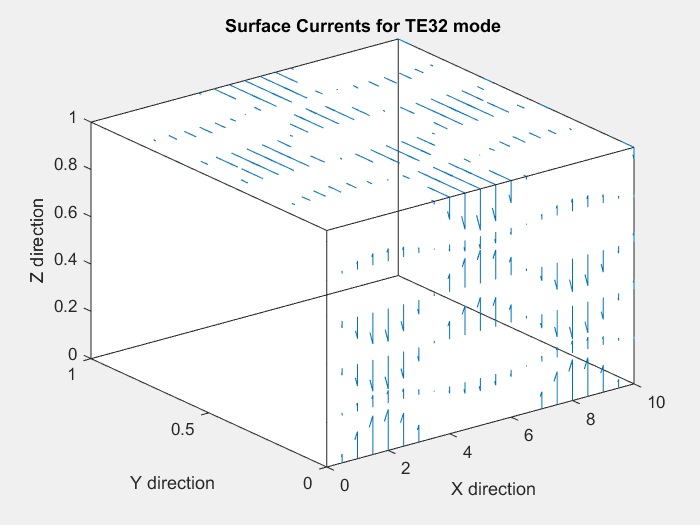
We can make the following observations from the above animation: