INTRODUCTION  TO TAGUCHI METHOD

Every experimenter has to plan and conduct experiments to obtain enough and relevant data so that he can infer the science behind the observed phenomenon. He can do so by,

(1) trial-and-error approach :
     ------------------------------

performing a series of experiments each of which gives some understanding. This requires making measurements after every experiment so that analysis of observed data will allow him to decide what to do next - "Which parameters should be varied and by how much". Many a times such series does not progress much as negative results may discourage or will not allow a selection of parameters which ought to be changed in the next experiment. Therefore, such experimentation usually ends well before the number of experiments reach a double digit! The data is insufficient to draw any significant conclusions and the main problem (of understanding the science) still remains unsolved.

(2) Design of experiments :
     -----------------------------

A well planned set of experiments, in which all parameters of interest are varied over a specified range, is a much better approach to obtain systematic data. Mathematically speaking, such a complete set of experiments ought to give desired results. Usually the number of experiments and resources (materials and time) required are prohibitively large. Often the experimenter decides to perform a subset of the complete set of experiments to save on time and money! However, it does not easily lend itself to understanding of science behind the phenomenon. The analysis is not very easy (though it may be easy for the mathematician/statistician) and thus effects of various parameters on the observed data are not readily apparent. In many cases, particularly those in which some optimization is required, the method does not point to the BEST settings of parameters. A classic example illustrating the drawback of design of experiments is found in the planning of a world cup event, say football. While all matches are well arranged with respect to the different teams and different venues on different dates and yet the planning does not care about the result of any match (win or lose)!!!! Obviously, such a strategy is not desirable for conducting scientific experiments (except for co-ordinating various institutions, committees, people, equipment, materials etc.).
 

(3) TAGUCHI Method :
     --------------------------

Dr. Taguchi of Nippon Telephones and Telegraph Company, Japan has developed a method based on " ORTHOGONAL ARRAY " experiments which gives much reduced " variance " for the experiment with " optimum settings " of control parameters. Thus the marriage of Design of Experiments with optimization of control parameters to obtain BEST results is achieved in the Taguchi Method. "Orthogonal Arrays" (OA) provide a set of well balanced (minimum) experiments and Dr. Taguchi's Signal-to-Noise ratios (S/N), which are log functions of desired output, serve as objective functions for optimization, help in data analysis and prediction of optimum results.

Taguchi Method treats optimization problems in two categories,
 

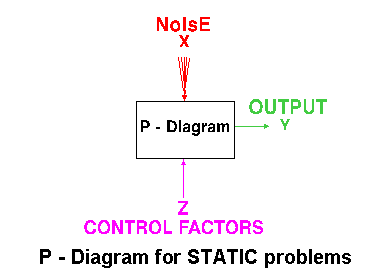
[A] STATIC PROBLEMS  :

Generally, a process to be optimized has several control factors which directly decide the target or desired value of the output. The optimization then involves determining the best control factor levels so that the output is at the the target value. Such a problem is  called as a "STATIC PROBLEM".

This is best explained using a P-Diagram which is shown below ("P" stands for Process or Product). Noise is shown to be present in the process but should have no effect on the output! This is the primary aim of the Taguchi experiments - to minimize variations in output even though noise is present in the process. The process is then said to have become ROBUST.
 

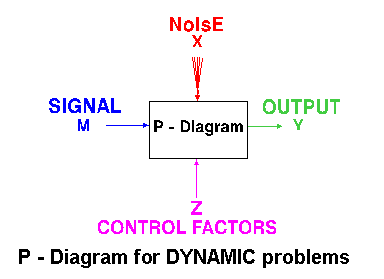
[B] DYNAMIC PROBLEMS :

If the product to be optimized has a signal input that directly decides the output, the optimization involves determining the best control factor levels so that the "input signal / output" ratio is closest to the desired relationship. Such a problem is called as a "DYNAMIC PROBLEM".
 

This is best explained by a P-Diagram which is shown below. Again, the primary aim of the Taguchi experiments - to minimize variations in output even though noise is present in the process- is achieved by getting improved linearity in the input/output relationship.
 

[A] STATIC PROBLEM  (BATCH PROCESS OPTIMIZATION) :
      ----------------------------------------------------------------------------

There are 3 Signal-to-Noise ratios of common interest for optimization of Static Problems;

(I) SMALLER-THE-BETTER :
    --------------------------------------

    n = -10 Log₁₀ [ mean of sum of squares of measured data ]

This is usually the chosen S/N ratio for all undesirable characteristics like " defects " etc. for which the ideal value is zero. Also, when an ideal value is finite and its maximum or minimum value is defined (like maximum purity is 100% or maximum Tc is 92K or minimum time for making a telephone connection is 1 sec) then the difference between measured data and ideal value is expected to be as small as possible. The generic form of S/N ratio then becomes,

    n = -10 Log₁₀ [ mean of sum of squares of {measured - ideal} ]
 

(II) LARGER-THE-BETTER :
     -------------------------------------

    n = -10 Log₁₀ [mean of sum squares of reciprocal of measured data]

This case has been converted to SMALLER-THE-BETTER by taking the reciprocals of measured data and then taking the S/N ratio as in the smaller-the-better case.
 

(III) NOMINAL-THE-BEST :
      -----------------------------------

                            square of mean
    n = 10 Log₁₀  -----------------
                                variance

This case arises when a specified value is MOST desired, meaning that neither a smaller nor a larger value is desirable.

    Examples are;

    (i) most parts in mechanical fittings have dimensions which are nominal-the-best type.

    (ii) Ratios of chemicals or mixtures are nominally the best type.

          e.g.     Aqua regia 1:3 of HNO3:HCL
                     Ratio of Sulphur, KNO3 and Carbon in gun powder

    (iii) Thickness should be uniform in deposition /growth /plating /etching..
 

[B] DYNAMIC PROBLEM  (TECHNOLOGY  DEVELOPMENT) :
      ------------------------------------------------------------------------------

In dynamic problems, we come across many applications where the output is supposed to follow input signal in a predetermined manner. Generally, a linear relationship between "input" "output" is desirable.
 

For example : Accelerator peddle in cars,
                      volume control in audio amplifiers,
                      document copier (with magnification or reduction)
                      various types of moldings
                      etc.

There are 2 characteristics of common interest in "follow-the-leader" or "Transformations" type of applications,

(i) Slope of the I/O characteristics

and

(ii) Linearity of the I/O characteristics
     (minimum deviation from the best-fit straight line)
 

The Signal-to-Noise ratio for these 2 characteristics have been defined as;
 

(I) SENSITIVITY {SLOPE}:
     ----------------------------------

Taguchi method is a scientifically disciplined mechanism for evaluating and implementing improvements in products, processes, materials, equipment, and facilities. These improvements are aimed at improving the desired characteristics and simultaneously reducing the number of defects by studying the key variables controlling the process and optimizing the procedures or design to yield the best results.

The method is applicable over a wide range of engineering fields that include processes that manufacture raw materials, sub systems, products for professional and consumer markets. In fact, the method can be applied to any process be it engineering fabrication, computer-aided-design, banking and service sectors etc. Taguchi method is useful for 'tuning' a given process for 'best' results.

Taguchi proposed a standard 8-step procedure for applying his method for optimizing any process,

8-STEPS  IN  TAGUCHI  METHODOLOGY:

Step-1: IDENTIFY  THE  MAIN  FUNCTION, SIDE  EFFECTS,  AND  FAILURE  MODE

Step-2: IDENTIFY  THE  NOISE  FACTORS, TESTING  CONDITIONS,  AND  QUALITY  CHARACTERISTICS

Step-3: IDENTIFY  THE  OBJECTIVE  FUNCTION  TO  BE  OPTIMIZED

Step-4: IDENTIFY  THE  CONTROL  FACTORS  AND  THEIR  LEVELS

Step-5: SELECT  THE  ORTHOGONAL  ARRAY  MATRIX  EXPERIMENT

Step-6: CONDUCT  THE  MATRIX  EXPERIMENT

Step-7: ANALYZE  THE  DATA, PREDICT  THE  OPTIMUM  LEVELS  AND  PERFORMANCE

Step-8: PERFORM  THE  VERIFICATION  EXPERIMENT AND  PLAN  THE  FUTURE  ACTION

SUMMARY :
 

Every experimenter develops a nominal process/product that has the desired functionality as demanded by users. Beginning with these nominal processes, he wishes to optimize the processes/products by varying the control factors at his disposal, such that the results are reliable and repeatable (i.e. show less variations).

In Taguchi Method, the word "optimization" implies "determination of BEST levels of control factors". In turn, the BEST levels of control factors are those that maximize the Signal-to-Noise ratios. The Signal-to-Noise ratios are log functions of desired output characteristics. The experiments, that are conducted to determine the BEST levels, are based on "Orthogonal Arrays", are balanced with respect to all control factors and yet are minimum in number. This in turn implies that the resources (materials and time) required for the experiments are also minimum.

Taguchi method divides all problems into 2 categories - STATIC or DYNAMIC. While the Dynamic problems have a SIGNAL factor, the Static problems do not have any signal factor. In Static problems, the optimization is achieved by using 3 Signal-to-Noise ratios - smaller-the-better, LARGER-THE-BETTER and nominal-the-best. In Dynamic problems, the optimization is achieved by using 2 Signal-to-Noise ratios - Slope and Linearity.

Taguchi Method is a process/product optimization method that is based on 8-steps of planning, conducting and evaluating results of matrix experiments to determine the best levels of control factors. The primary goal is to keep the variance in the output very low even in the presence of noise inputs. Thus, the processes/products are made ROBUST against all variations.
 

- - end of Intro - -
 

Read an Intro meant for Indian Industry

Go back to Taguchi Page

Go back to Apte's web-page
 
 
 

modified 26-Aug-2000  /  3-Oct-2000 / 14-Dec-2000