Stream and Block Cipher Constructions

Saravanan Vijayakumaran

Department of Electrical Engineering, IIT Bombay

September 11, 2024

Stream Ciphers

  • Used in practice to instantiate pseudorandom generators

  • A stream cipher is a pair of deterministic algorithms (\textsf{Init}, \textsf{Next})

    • \textsf{Init} takes as input a seed s and an optional initialization vector IV, and outputs some initial state \textsf{st}
    • \textsf{Next} takes as input a current state \textsf{st} and outputs a bit y along with updated state \textsf{st}'

  • Starting from some initial state \textsf{st}_0, any number of bits can be generated by repeatedly invoking \textsf{Next}

A5/1

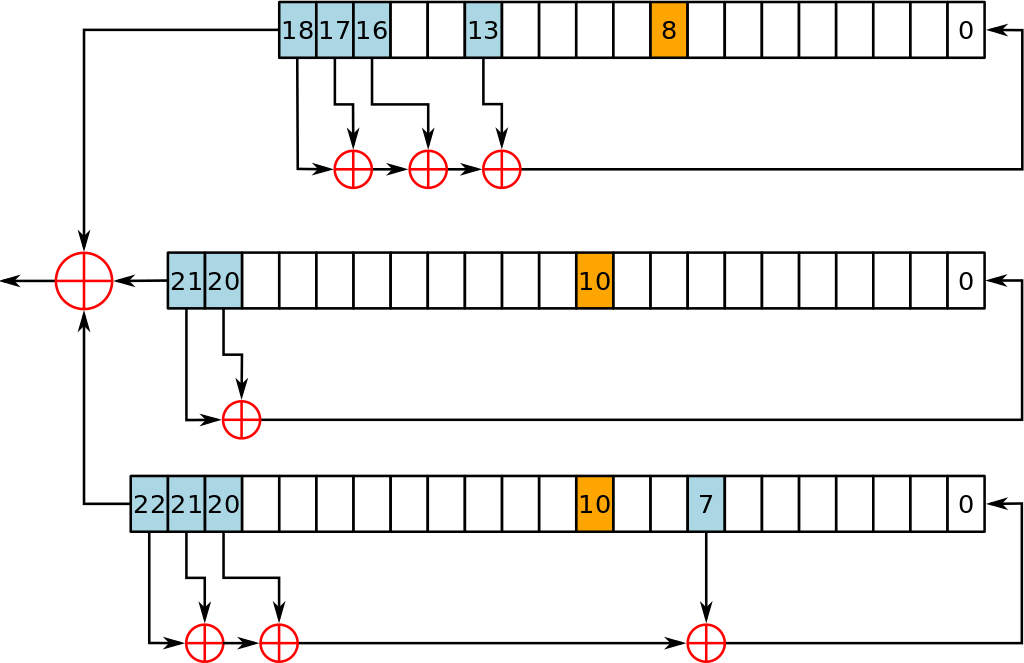
Image credit: Wikipedia

Trivium

  • Stream cipher developed in 2005 by Christophe de Cannière and Bart Preneel
  • Has three nonlinear feedback shift registers having sizes 93, 84, and 111 (total 288 bits)
  • Trivium = Latin for “the three-fold way”
  • No attacks better than exhaustive search are known

Trivium Initialization

  • Trivium accepts a 80-bit key and 80-bit IV

    • Let K_1, K_2, \ldots, K_{80} be the key bits
    • Let IV_1, IV_2, \ldots, IV_{80} be the IV bits

  • Let s_1, s_2,\ldots, s_{288} be the 288 bits of state

Trivium Initialization

  • (s_1, s_2, \ldots, s_{93}) \leftarrow (K_1, K_2, \ldots, K_{80}, 0,\ldots,0)

  • (s_{94}, s_{95}, \ldots, s_{177}) \leftarrow (IV_1, \ldots, IV_{80}, 0,\ldots,0)

  • (s_{178}, s_{179}, \ldots, s_{288}) \leftarrow (0,\ldots,0,1,1,1)

  • for i=1, 2, \ldots, 1152 do

    • t_1 \leftarrow s_{66} \oplus (s_{91} \wedge s_{92}) \oplus s_{93} \oplus s_{171}
    • t_2 \leftarrow s_{162} \oplus (s_{175} \wedge s_{176}) \oplus s_{177}\oplus s_{264}
    • t_3 \leftarrow s_{243} \oplus (s_{286} \wedge s_{287}) \oplus s_{288}\oplus s_{69}
    • (s_1, s_2, \ldots, s_{93}) \leftarrow (t_3, s_1,\ldots,s_{92})
    • (s_{94}, s_{95}, \ldots, s_{177}) \leftarrow (t_1, s_{94}, \ldots, s_{176})
    • (s_{178}, s_{179}, \ldots, s_{288}) \leftarrow (t_2, s_{178}, \ldots, s_{287})

Trivium Output

  • At a given state (s_1, s_2, \ldots, s_{288}), the next N output bits z_1, z_2,\ldots, z_N are obtained as follows
  • for i=1, 2, \ldots, N do
    • a \leftarrow s_{66} \oplus s_{93}, b \leftarrow s_{162} \oplus s_{177}, c \leftarrow s_{243} \oplus s_{288}
    • z_i \leftarrow a \oplus b \oplus c
    • t_1 \leftarrow a \oplus (s_{91} \wedge s_{92}) \oplus s_{171}
    • t_2 \leftarrow b \oplus (s_{175} \wedge s_{176}) \oplus s_{264}
    • t_3 \leftarrow c \oplus (s_{286} \wedge s_{287}) \oplus s_{69}
    • (s_1, s_2, \ldots, s_{93}) \leftarrow (t_3, s_1,\ldots,s_{92})
    • (s_{94}, s_{95}, \ldots, s_{177}) \leftarrow (t_1, s_{94}, \ldots, s_{176})
    • (s_{178}, s_{179}, \ldots, s_{288}) \leftarrow (t_2, s_{178}, \ldots, s_{287})

Trivium

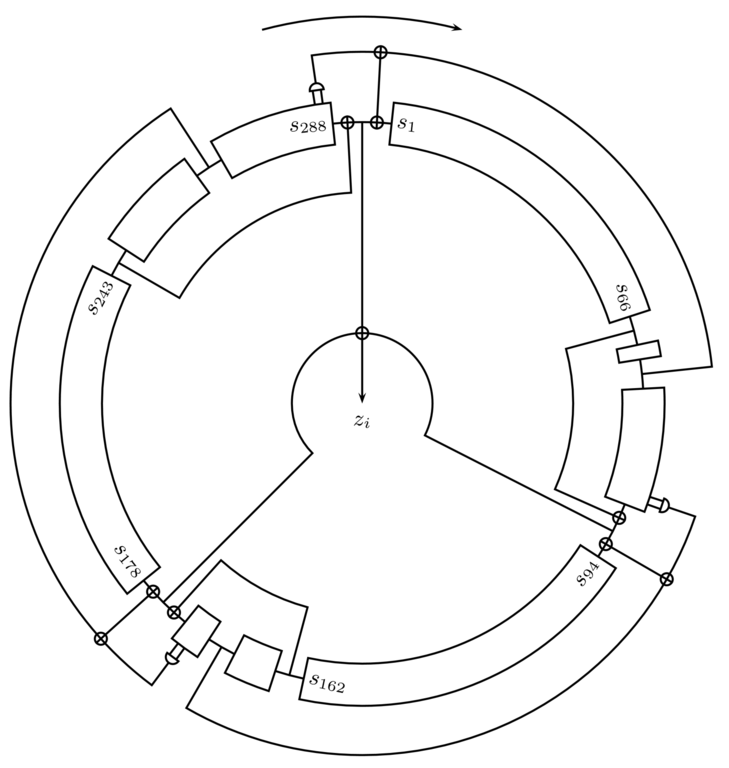
Image credit: Wikipedia

RC4

  • Shift register based ciphers are efficient in hardware implementation but have poor performance in software

  • RC4 was designed by Ron Rivest in 1984 for good software performance

  • No longer recommended due to recent attacks

  • State of RC4

    • A 256-byte array S, which contains a permutation of 0,1,\ldots,255
    • Two integers i,j \in \{0,1,\ldots,255\}

RC4 Initialization

  • Input: 16-byte key k, Output: Initial state (S, i, j)

    \begin{align*} &\textbf{for } i=0,1,\ldots,255\\ & \quad\quad S[i] \coloneqq i\\ & \quad\quad k[i] \coloneqq k[i \bmod 16]\\ & j \coloneqq 0\\ &\textbf{for } i=0,1,\ldots,255\\ &\quad\quad j \coloneqq j + S[i] + k[i]\\ &\quad\quad \text{Swap } S[i] \text{ and } S[j]\\ &i \coloneqq 0, \quad j \coloneqq 0\\ & \textbf{return } (S, i, j) \end{align*}

RC4 Next Byte

  • Input: Current state (S,i,j)

  • Output: Output byte y and updated (S, i, j)

    \begin{align*} &i \coloneqq i + 1\\ &j \coloneqq j + S[i]\\ &\text{Swap } S[i] \text{ and } S[j]\\ &t \coloneqq S[i] + S[j]\\ &y \coloneqq S[t] \\ & \textbf{return } y \text{ and } (S, i, j) \end{align*}

Block Ciphers

  • Used to instantiate pseudorandom permutations
  • Typically constructed using substitution-permutation networks

The Confusion-Diffusion Paradigm

  • Idea: Construct a random-looking permutation with a large block length from many smaller permutations
  • Suppose we want to construct F with block length 128
  • The key k will specify 16 permutations f_1, f_2, \ldots, f_{16} each having block length 8
  • For x \in \{0,1\}^{128}, parse x into bytes x_1, x_2,\ldots, x_{16} F_k(x) = f_1(x_1) \| f_2(x_2) \| \cdots \| f_{16}(x_{16})
  • The functions \{f_i\} are said to introduce confusion
  • The diffusion step involves permuting the bits in F_k(x)

Substitution-Permutation Networks

  • An implementation of the confusion-diffusion paradigm

  • The confusion functions are independent of the key

  • Consider an SPN with block length 64. For input x, do

    1. Key mixing: Set x \coloneqq x \oplus k where k is the round key
    2. Substitution: Set x \coloneqq S_1(x_1) \| S_2(x_2) \| \cdots \| S_8(x_8) where x_i is the ith byte of x
    3. Permutation: Permute the bits of x to obtain the output of the round

One Round of the SPN

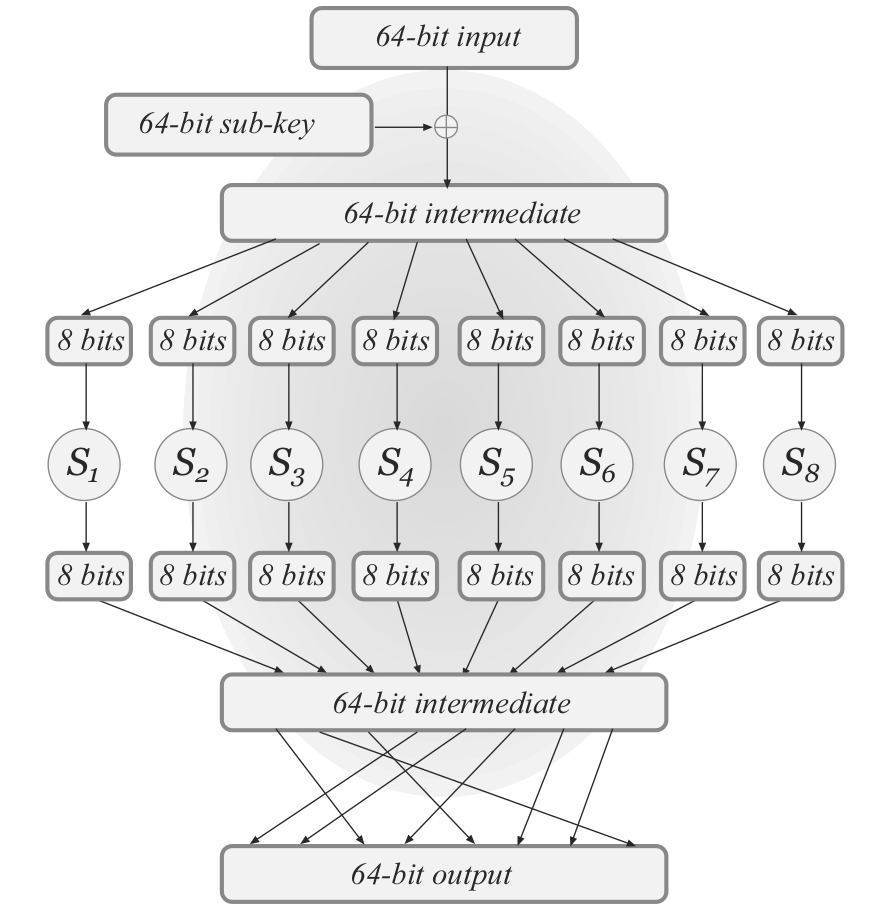
Image credit: Katz & Lindell

Data Encryption Standard

  • Block cipher developed in the 1970s by IBM and adopted by the US in 1977 as a FIPS
  • Block length is 64 bits and key length is 56 bits
  • No longer considered secure due to 56-bit key length
  • Superseded by AES in 2000

Feistel Networks

  • A method to construct an invertible function from non-invertible components

DES is a 16-round Feistel network

DES Initial Permutation

Image credit: Wikipedia

DES Round Function

DES Key Schedule

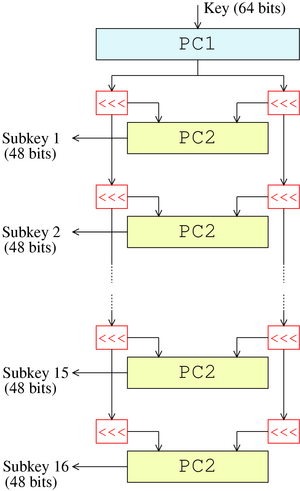
Image credit: Wikipedia

References