Introduction and Classical Cryptography

Saravanan Vijayakumaran

Department of Electrical Engineering, IIT Bombay

July 31, 2024

Lecture Plan

Describe the difference between modern and classical cryptography
Describe the syntax of private-key encryption
Describe some classical ciphers – Caesar cipher, Substitution cipher, Vigenère cipher

Cryptography

Dictionary definition: “the art of writing or solving codes”
- Historically accurate but does not convey the current breadth of the field
- Codes refers to schemes used for secret communication (encryption)
In addition to encryption, cryptography today deals with
- mechanisms for ensuring integrity,
- techniques for exchanging secret keys,
- protocols for authenticating users,
- electronic voting,
- cryptocurrency, and more.
Modern definition: the study of mathematical techniques for securing digital information, systems, and distributed computations against adversarial attacks.

Modern Cryptography

Modern cryptography = post-1980s cryptography
In the 1970s and 1980s, a rich theory emerged changing cryptography from an art to a science
Modern approach to cryptography
- Formal definitions
- Precise assumptions
- Proofs of security

Private-key Encryption Setting

Two parties want to communicate over a channel which is monitored by an eavesdropper
They want to keep their messages hidden from the eavesdropper
A secret (the key) is shared by the communicating parties in advance and unknown to the eavesdropper
The workflow
- When a party wants to send a message (plaintext) to the other, they use the shared key to encrypt the message and obtain a ciphertext
- The ciphertext is transmitted over the channel and observed by the eavesdropper
- The receiver uses the same shared key to decrypt the ciphertext and recover the plaintext
- The same key is used for both encryption and decryption; so this setting is also called the symmetric-key setting
Communicating parties could be separated in space or time
- Key sharing becomes trivial in the latter situation

The Syntax of Encryption

A private-key encryption scheme is defined by specifying a message space \mathcal{M} along with three algorithms:
- A procedure for generating keys (\texttt{Gen}),
- A procedure for encrypting (\texttt{Enc})
- A procedure for decrypting (\texttt{Dec})
The message space \mathcal{M} defines the set of allowed messages
The algorithms of the scheme have the following functionality:
1. \texttt{Gen} is a probabilistic algorithm that outputs a key k chosen according to some distribution.
2. \texttt{Enc} takes as input a key k and a message m and outputs a ciphertext c.
  - \texttt{Enc}_k (m) denotes the encryption of the plaintext m using the key k
3. \texttt{Dec} takes as input a key k and a ciphertext c and outputs a plaintext m.
  - \texttt{Dec}_k (c) denotes the decryption of the ciphertext c using the key k
An encryption scheme must satisfy the following correctness requirement: for every key k output by \texttt{Gen} and every message m \in \mathcal{M}, it holds that \texttt{Dec}_k (\texttt{Enc}_k (m)) = m.
The set of all possible keys \mathcal{K} is called the key space
- Almost always, \texttt{Gen} chooses a key uniformly from \mathcal{K}

Kerckhoffs’ Principle

The communicating parties must keep the key k secret
Should they also keep the details of the encryption and decryption also a secret?
In the late 19th century, Auguste Kerckhoffs argued against doing this

The cipher method must not be required to be secret, and it must be able to fall into the hands of the enemy without inconvenience.
Kerckhoffs’ Principle: Security relies solely on secrecy of key
Three reasons
- Easier to keep a short key secret than to keep an algorithm secret
- Easier to change key than encryption scheme
- Standardization is easier

Historical Ciphers

Caesar’s Cipher

Julius Caesar encrypted by shifting the letters of the alphabet 3 places forward
- a was replaced with D, b with E, and so on
- In the rest of this lecture, we will use lower case letters for plaintext and uppercase letters for ciphertext
Encryption of the message begin the attack now gives EHJLQWKHDWWDFNQRZ
There is no key. Anyone learning how it works can decrypt the ciphertext
A variant of this cipher called ROT-13 is used nowadays in social media
- Used to make information like movie spoilers unintelligible for casual readers

The Shift Cipher

Keyed variant of Caesar’s cipher
Key k is a number between 0 and 25
\texttt{Gen} outputs a uniform key k \in \{0, . . . , 25\}
\texttt{Enc} takes a key k and a plaintext and shifts each letter of the plaintext forward k positions (wrapping around at the end of the alphabet)
\texttt{Dec} takes a key k and a ciphertext and shifts every letter of the ciphertext backward k positions.

Mathematical Description of the Shift Cipher

Equate the English alphabet with the set \{0, . . . , 25\} (so a = 0, b = 1, etc.).
Message space \mathcal{M} is then any finite sequence of integers from this set.
Encryption of the message m = m_1 \cdots m_l (where m_i \in \{0, . . . , 25\}) using key k is given by \texttt{Enc}_k (m_1 \cdots m_l ) = c_1 \cdots c_l, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ where } c_i = [(m_i + k) \bmod 26].
The notation [a \bmod N ] denotes the remainder of a upon division by N , with 0 \leq [a \bmod N ] < N.
We refer to the process mapping a to [a \bmod N] as reduction modulo N.
Decryption of a ciphertext c = c_1 \cdots c_l where key k is given by \texttt{Dec}_k (c_1 \cdots c_l ) = m_1 \cdots m_l, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ where } m_i = [(c_i - k) \bmod 26].

The Sufficient Key-Space Principle

When the shift cipher is used, is it possible to recover the message without knowing k?
Yes! Because that there are only 26 possible keys.
Try every possible key and choose the plaintext that “makes sense”
An attack that involves trying every possible key is called a brute-force or exhaustive-search attack. Clearly, for an encryption scheme to be secure it must not be vulnerable to such an attack.
The sufficient key-space principle:

Any secure encryption scheme must have a key space that is sufficiently large to make an exhaustive-search attack infeasible.
What is considered “infeasible”? Key space should have size at least 2^{80}
Above principle gives a necessary condition for security, but not a sufficient one.

The Mono-alphabetic Substitution Cipher

In the shift cipher, the key defines a map from each letter of the alphabet to some letter of the alphabet, where the map is a fixed shift
In the mono-alphabetic substitution cipher, the key is a bijection from \{a,b,\ldots,z\} to \{a,b,\ldots,z\}
So, for example, the key that defines the following permutation

a b c d e f g h i j k l m

X E U A D N B K V M R O C

n o p q r s t u v w x y z

Q F S Y H W G L Z I J P T
The message helloworld would be encrypted as KDOOFIFHOA
The key space thus consists of all bijections, or permutations, of the alphabet.
The key space is of size 26! = 26 · 25 · 24 · · · 2 · 1 \approx 2^{88}. So a brute-force attack is infeasible.
This, however, does not mean the cipher is secure!

Breaking the Substitution Cipher

Assume English-language text is being encrypted (i.e., grammatically correct English writing)
The attack uses statistical properties of the English language.
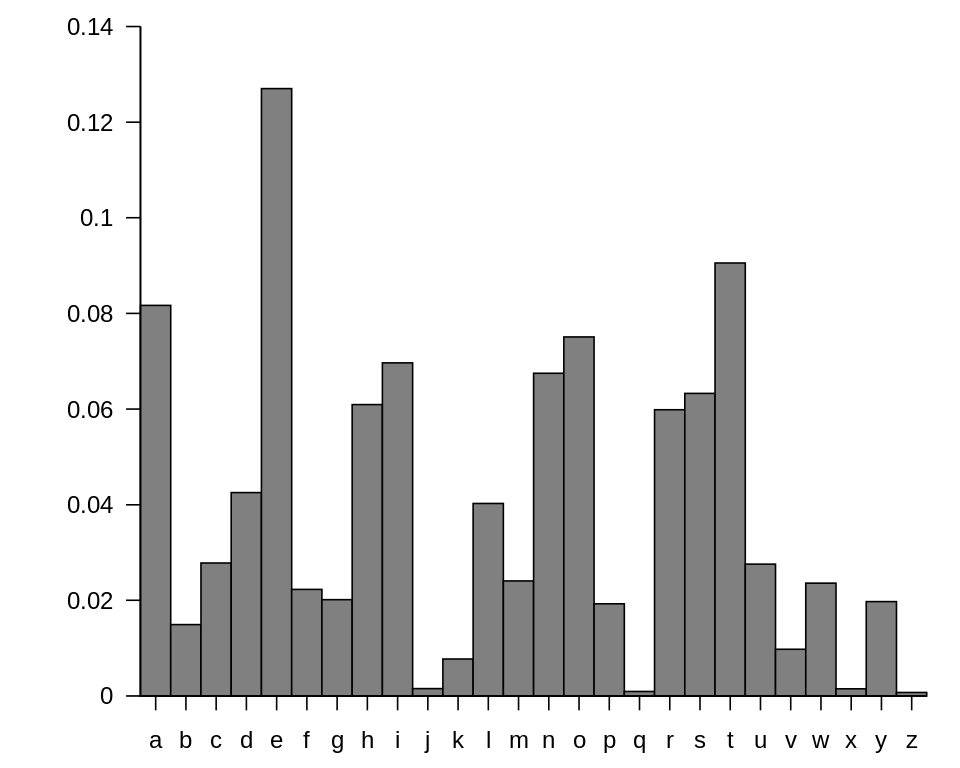
The frequency distribution of individual letters in English-language text is known

Average letter frequencies for English-language text. Source: Wikipedia
Calculate frequency of letters in the ciphertext and try guessing the bijection

The Vigenère Cipher

The statistical attack on the mono-alphabetic substitution cipher works because the key defines a fixed mapping
Such an attack fails against poly-alphabetic substitution cipher; apply mapping to blocks of plaintext
The Vigenère cipher, is a type of poly-alphabetic shift cipher
The key is as a string of letters
Encryption is done by shifting each plaintext character by the amount indicated by the next character of the key, wrapping around in the key when necessary.
For example, encryption of the message tellhimaboutme using the key cafe would work as follows:

Vigenère cipher example

Plaintext tellhimaboutme

Key (repeated) cafecafecafeca

Ciphertext VEQPJIREDOZXOE
Was considered to be “unbreakable”
Invented in the 16th century; a systematic attack was only devised hundreds of years later

Vigenère cipher example
Plaintext	`tellhimaboutme`
Key (repeated)	`cafecafecafeca`
Ciphertext	`VEQPJIREDOZXOE`

Attacking the Vigenère cipher

Observation: If the length of the key is known then attacking the cipher is relatively easy
Let the length of the key, also called the period, be t.
Write the key k as k = k_1 \cdots k_t where each k_i is a letter of the alphabet.
An observed ciphertext c = c_1 c_2 \cdots can be divided into t parts where each part can be viewed as having been encrypted using the shift cipher.
Apply the shift cipher attack on each of the t streams.
What if the key length is unknown?
As long as the maximum length T of the key is not too large, repeat the above attack T times
- Once for each possible value t \in \{1, . . . , T \})
Kasiski’s method, published in the mid-19th century, is a better method

Conclusions

Designing secure ciphers is hard
A complex scheme is not necessarily secure
All historical schemes have been broken

Introduction and Classical Cryptography

Lecture Plan

Cryptography

Modern Cryptography

Private-key Encryption Setting

The Syntax of Encryption

Kerckhoffs’ Principle

Historical Ciphers

Caesar’s Cipher

The Shift Cipher

Mathematical Description of the Shift Cipher

The Sufficient Key-Space Principle

The Mono-alphabetic Substitution Cipher

Breaking the Substitution Cipher

The Vigenère Cipher

Attacking the Vigenère cipher

Conclusions

Further Reading