Public-Key Encryption

Saravanan Vijayakumaran

Department of Electrical Engineering, IIT Bombay

October 23, 2024

Public-Key Encryption Workflow

Suppose Bob wants to send a message to Alice
Alice will generate a public-private key-pair (pk_A, sk_A)
- The private key is also called the secret key
Alice will share pk_A with Bob over the public channel
Bob will encrypt a message m as c \leftarrow \textsf{Enc}_{pk_A}(m) and send c to Alice over the public channel
Alice will decrypt c using her private key sk_A

Why bother with private-key encryption?

Public-key encryption is 2-3 orders of magnitude slower than private-key encryption
Hybrid encryption is often used in practice
Here \textsf{Enc} is a public-key encryption scheme and \textsf{Enc}' is a private-key encryption scheme

Public-Key Encryption Schemes

A public-key encryption scheme is a triple of PPT algorithms (\textsf{Gen}, \textsf{Enc}, \textsf{Dec}) such that:
1. (pk,sk) \leftarrow \textsf{Gen}(1^n)
  - pk is the public key and sk is the private key
  - The public key defines a message space \mathcal{M}_{pk}
2. For m \in \mathcal{M}_{pk}, c \leftarrow \textsf{Enc}_{pk}(m).
3. m \coloneqq \textsf{Dec}_{sk}(c), where m \in \mathcal{M}_{pk} \cup \{\perp\}.
It is required that \textsf{Dec}_{sk}\left( \textsf{Enc}_{pk}\left( m \right) \right) = m for any message m \in \mathcal{M}_{pk}, except with negligible probability over the randomness of \textsf{Enc} and \textsf{Dec}

CPA Security

Eavesdropping Indistinguishability Experiment

Consider the following experiment \textsf{PubK}^{\textsf{eav}}_{\mathcal{A}, \Pi}(n):
- \textsf{Gen}(1^n) is run to obtain keys (pk, sk)
- \mathcal{A} is given pk and outputs a pair of equal-length messages m_0, m_1 \in \mathcal{M}_{pk}
- A uniform bit b \in \{0,1\} is chosen
- Challenge ciphertext c \leftarrow \textsf{Enc}_k(m_b) is computed and given to \mathcal{A}
- \mathcal{A} outputs a bit b'
- The output of the experiment is defined to be 1 if b' = b, and 0 otherwise

Security Definition

A public-key encryption scheme \Pi = (\textsf{Gen}, \textsf{Enc}, \textsf{Dec}) has indistinguishable encryptions in the presence of an eavesdropper, or is EAV-secure, if for all PPT adversaries \mathcal{A} there is a negligible function \textsf{negl} such that, for all n, \Pr\left[ \textsf{PubK}^{\textsf{eav}}_{\mathcal{A},\Pi}(n) = 1\right] \le \frac{1}{2} + \textsf{negl}(n).

CPA-Security for Public-Key Encryption

In public-key encryption, the adversary always has access to an encryption oracle
Proposition: If a public-key encryption scheme has indistinguishable encryptions in the presence of an eavesdropper, it is CPA-secure

El Gamal Encryption (1/2)

In 1985, Taher El Gamal constructed a public-key encryption scheme based on the Diffie-Hellman protocol
\textsf{Gen}:
- Run \mathcal{G}(1^n) to get (G, q, g).
- Choose a uniform x \in \mathbb{Z}_q and compute h \coloneqq g^x.
- The public key is \langle G, q, g, h \rangle and the private key is \langle G, q, g, x\rangle.
- The message space is G

El Gamal Encryption (2/2)

\textsf{Enc}:
- For public key pk =\langle G, q, g, h \rangle and message m \in G, choose a uniform y \in \mathbb{Z}_q
- Output the ciphertext as \langle g^y, h^y \cdot m \rangle
\textsf{Dec}:
- For public key pk =\langle G, q, g, h \rangle and ciphertext \langle c_1, c_2 \rangle, output \hat{m} = c_2 \cdot c_1^{-x}.

CPA-Security of El Gamal Encryption

Theorem: If the DDH problem is hard relative to \mathcal{G}, then the El Gamal encryption scheme is CPA-secure.
Proof
- Consider a modified “encryption scheme” \widetilde{\Pi} where the encryption of message m wrt public key \langle G, q, g, h \rangle is as follows
- Choose uniform y,z \in \mathbb{Z}_q and output ciphertext \langle g^y, g^z \cdot m \rangle.

CPA-Security of El Gamal Encryption

Consider the following PPT algorithm D that attempts to solve the DDH problem
1. D is given (G, q, g, h_1, h_2, h_3) as input
2. Set pk = \langle G, q, g, h_1 \rangle and run \mathcal{A}(pk) to obtain two messages m_0, m_1 \in G
3. Choose a uniform bit b
4. Set c_1 \coloneqq h_2 and c_2 \coloneqq h_3 \cdot m_b
5. Give the ciphertext \langle c_1, c_2 \rangle to \mathcal{A} and obtain a bit b'.
6. If b' = b, output 1; otherwise, output 0.

CPA-Security of El Gamal Encryption

Case 1: h_3 = g^z for uniform z \in \mathbb{Z}_q
- \langle c_1, c_2 \rangle = \langle g^y, g^z \cdot m_b \rangle
- \mathcal{A} experiences the experiment \textsf{PubK}^{\textsf{eav}}_{\mathcal{A},\widetilde{\Pi}}(n)
- Since D outputs 1 exactly when b' = b, we have \begin{align*} & \Pr\left[ D(G, q, g, g^x, g^y, g^z) =1 \right] \\ &= \Pr \left[ \textsf{PubK}^{\textsf{eav}}_{\mathcal{A}, \widetilde{\Pi}}(n)=1\right]= \frac{1}{2} \end{align*}

CPA-Security of El Gamal Encryption

Case 2: h_3 = g^{xy}
- \langle c_1, c_2 \rangle = \langle g^y, g^{xy} \cdot m_b \rangle
- \mathcal{A} experiences the experiment \textsf{PubK}^{\textsf{eav}}_{\mathcal{A},\Pi}(n)
- Since D outputs 1 exactly when b' = b, we have \begin{align*}& \Pr\left[ D(G, q, g, g^x, g^y, g^{xy}) =1 \right] \\ &= \Pr \left[ \textsf{PubK}^{\textsf{eav}}_{\mathcal{A}, \Pi}(n)=1\right] \end{align*}

CPA-Security of El Gamal Encryption

For any PPT distinguisher D, we have \begin{align*} &|\Pr\left[ D(G, q, g, g^x, g^y, g^{xy}) =1 \right]\\ &- \Pr\left[ D(G, q, g, g^x, g^y, g^{z}) =1 \right]| \le \textsf{negl}(n) \end{align*}
This implies that \begin{align*} &\left|\Pr \left[ \textsf{PubK}^{\textsf{eav}}_{\mathcal{A}, \Pi}(n)=1\right] - \frac{1}{2}\right| \le \textsf{negl}(n)\\ \implies & \Pr \left[ \textsf{PubK}^{\textsf{eav}}_{\mathcal{A}, \Pi}(n)=1\right] \le \frac{1}{2} + \textsf{negl}(n) \end{align*}

Multiple Encryptions

Can we guarantee security when the same key is used to encrypt multiple messages?
Surprisingly, CPA-security for one message implies CPA-security for multiple messages

Defining CPA-Security for Multiple Encryptions

We could define an experiment as follows
- An adversary \mathcal{A} picks two lists of messages \begin{align*} \vec{m}_0 &= \langle m_{0,1}, m_{0,2},\ldots,m_{0,l} \rangle\\ \vec{m}_1 &= \langle m_{1,1}, m_{1,2},\ldots,m_{1,l} \rangle \end{align*}
- A uniform bit b is chosen
- The challenge ciphertext is the encryption of \vec{m}_b
But this does not allow \mathcal{A} to adaptively choose the messages

The Left-or-Right Oracle

On input a pair of equal-length messages m_0, m_1, oracle \textsf{LR}_{pk,b}(\cdot, \cdot) returns the ciphertext c \leftarrow \textsf{Enc}_{pk}(m_b)
Access to this oracle allows \mathcal{A} to adaptively choose the messages used to produce the challenge ciphertext

LR-Oracle Experiment

Consider the following experiment \textsf{PubK}^{\textsf{LR-cpa}}_{\mathcal{A}, \Pi}(n):
- A keypair (pk,sk) is generated using \textsf{Gen}(1^n)
- A uniform bit b \in \{0,1\} is chosen
- \mathcal{A} is given 1^n and oracle access to \textsf{LR}_{pk,b}(\cdot,\cdot)
- \mathcal{A} outputs a bit b'
- The output of the experiment is 1 if b' = b, and 0 otherwise

Security Definition

A public-key encryption scheme \Pi = (\textsf{Gen}, \textsf{Enc}, \textsf{Dec}) has indistinguishable multiple encryptions if for all PPT adversaries \mathcal{A} there is a negligible function \textsf{negl} such that \Pr\left[ \textsf{PubK}^{\textsf{LR-cpa}}_{\mathcal{A},\Pi}(n) = 1\right] \le \frac{1}{2} + \textsf{negl}(n).

CPA-Security \implies Indistinguishable Multiple Encryptions

Theorem: If public-key encryption scheme \Pi is CPA-secure, then it also has indistinguishable multiple encryptions
Consequently, all the following security definitions are equivalent
1. Indistinguishable encryptions in the presence of an eavesdropper
2. CPA-security
3. Indistinguishable multiple encryptions

Proof (1/7)

Let \Pi be a CPA-secure public-key encryption scheme
Let \mathcal{A} be an arbitrary PPT adversary in the \textsf{PubK}^{\textsf{LR-cpa}}_{\mathcal{A},\Pi}(n) experiment
We want to show that \Pr\left[ \textsf{PubK}^{\textsf{LR-cpa}}_{\mathcal{A},\Pi}(n) =1\right] \le \frac{1}{2} + \textsf{negl}(n)

Proof (2/7)

Let t = t(n) be the number of oracle queries made by \mathcal{A}
For 0 \le i \le t, let \textsf{LR}_{pk}^i be the oracle that on input (m_0, m_1)
- Returns \textsf{Enc}_{pk}(m_0) for the first i queries
- Returns \textsf{Enc}_{pk}(m_1) for the next t-i queries
Note that \Pr\left[ \textsf{PubK}^{\textsf{LR-cpa}}_{\mathcal{A},\Pi}(n) =1\right] = \frac{1}{2} \Pr\left[\mathcal{A}^{\textsf{LR}_{pk}^t}(pk) = 0\right] \\+\frac{1}{2} \Pr\left[\mathcal{A}^{\textsf{LR}_{pk}^0}(pk) = 1\right]
It is enough to show that \bigg| \Pr\left[\mathcal{A}^{\textsf{LR}_{pk}^t}(pk) = 1\right] - \Pr\left[\mathcal{A}^{\textsf{LR}_{pk}^0}(pk) = 1\right]\bigg|\\ \le \textsf{negl}(n)

Proof (3/7)

Consider an adversary \mathcal{A}' that eavesdrops on the encryption of a single message
It will use the adversary \mathcal{A} of the \textsf{PubK}^{\textsf{LR-cpa}}_{\mathcal{A},\Pi}(n) experiment as a subroutine
Note the IO interfaces of the two adversaries
- \mathcal{A} queries the \textsf{LR}_{pk,b}(\cdot, \cdot) oracle t times. It then outputs a bit
- \mathcal{A}' outputs a pair of messages (m_0, m_1) and receives the encryption of one of them as a challenge ciphertext. It then outputs a bit.

Proof (4/7)

Consider an adversary \mathcal{A}' that does the following
1. \mathcal{A}', given pk, chooses a uniform index i \leftarrow \{1,\ldots,t\}
2. \mathcal{A}' runs \mathcal{A}(pk), answering its jth oracle query (m_{j,0}, m_{j,1}) as follows:
  1. For j <i, adversary \mathcal{A}' computes c_j \leftarrow \textsf{Enc}_{pk}(m_{j,0}) and returns c_j to \mathcal{A} as the response from its oracle
  2. For j =i, adversary \mathcal{A}' outputs (m_{j,0}, m_{j,1}) and receives a challenge ciphertext c_j. This is returned to \mathcal{A} as the response from its oracle
  3. For j >i, adversary \mathcal{A}' computes c_j \leftarrow \textsf{Enc}_{pk}(m_{j,1}) and returns c_j to \mathcal{A} as the response from its oracle
3. \mathcal{A}' outputs the bit b' that is output by A

Proof (5/7)

Consider the experiment \textsf{PubK}^{\textsf{eav}}_{\mathcal{A}',\Pi}
Fixing some i=i^*, note that if c_{i^*} is the encryption of m_{i^*,0} then \mathcal{A} is interacting with \textsf{LR}_{pk}^{i^*}
Then we have \begin{align*} & \Pr \left[ \mathcal{A}' \text{ outputs } 1 \mid b = 0\right] \\ & = \sum_{i^*=1}^t \Pr[i=i^*]\Pr \left[ \mathcal{A}' \text{ outputs } 1 \mid b = 0 \cap i = i^*\right] \\ & = \sum_{i^*=1}^t \frac{1}{t}\Pr \left[ \mathcal{A}^{\textsf{LR}_{pk}^{i^*}}(pk)=1\right] \\ \end{align*}

Proof (6/7)

If c_{i^*} is the encryption of m_{i^*,1} then \mathcal{A} is interacting with \textsf{LR}_{pk}^{i^*-1}
Then we have \begin{align*} & \Pr \left[ \mathcal{A}' \text{ outputs } 1 \mid b = 1\right] \\ & = \sum_{i^*=1}^t \Pr[i=i^*]\Pr \left[ \mathcal{A}' \text{ outputs } 1 \mid b = 1 \cap i = i^*\right] \\ & = \sum_{i^*=1}^t \frac{1}{t}\Pr \left[ \mathcal{A}^{\textsf{LR}_{pk}^{i^*-1}}(pk)=1\right] \\ & = \sum_{i^*=0}^{t-1} \frac{1}{t}\Pr \left[ \mathcal{A}^{\textsf{LR}_{pk}^{i^*}}(pk)=1\right] \\ \end{align*}

Proof (7/7)

Since \Pi is CPA-secure, we have \begin{align*}&\bigg| \Pr\left[ \mathcal{A}' \text{ outputs } 1 \mid b=0\right] \\ &\quad - \Pr\left[ \mathcal{A}' \text{ outputs } 1 \mid b=1\right]\bigg| \le \textsf{negl}(n)\end{align*}
This gives us \bigg| \Pr\left[\mathcal{A}^{\textsf{LR}_{pk}^t}(pk) = 1\right] - \Pr\left[\mathcal{A}^{\textsf{LR}_{pk}^0}(pk) = 1\right]\bigg|\\ \le t \cdot \textsf{negl}(n)

Plain RSA

Plain RSA Key Generation

Let \textsf{GenRSA} be a PPT algorithm that on input 1^n, outputs a modulus N that is the product of two n-bit primes, along with integers e,d > 1 satisfying ed = 1 \bmod \phi(N)
\textsf{Gen:} On input 1^n, run \textsf{GenRSA}(1^n) to obtain N, e, and d
- The public key is \langle N,e \rangle and the private key is \langle N,d \rangle.

Plain RSA Encryption and Decryption

\textsf{Enc:} On input a public key pk = \langle N,e \rangle and message m \in \mathbb{Z}_N^*, compute the ciphertext c = m^e \bmod N
\textsf{Dec:} On input a private key sk = \langle N, d \rangle and ciphertext c \in \mathbb{Z}_N^*, output \hat{m} = c^d \bmod N

The RSA Experiment

\textsf{RSA-inv}_{\mathcal{A}, \textsf{GenRSA}}(n):
- Run \textsf{GenRSA}(1^n) to obtain (N,e,d)
- Choose a uniform y \in \mathbb{Z}_N^*
- \mathcal{A} is given N,e,y, and outputs x \in \mathbb{Z}_N^*
- The output of the experiment is 1 if x^e = y \bmod N, and 0 otherwise.

The RSA Assumption

Definition: The RSA problem is hard relative to \textsf{GenRSA} if for all PPT algorithms \mathcal{A} there exists a negligible function \textsf{negl} such that \Pr[\textsf{RSA-inv}_{\mathcal{A}, \textsf{GenRSA}}(n) = 1] \le \textsf{negl}(n).
The RSA assumption states that there exists a \textsf{GenRSA} relative to which RSA is hard.

Attacks on Plain RSA

Plain RSA is deterministic and hence not CPA-secure
It is insecure even if used to encrypt “random messages”

Quadratic Improvement in Recovering Message (1/2)

Suppose an attacker knows that m < B
Given ciphertext c, the attacker can always determine m in \mathcal{O}(B) time
There is a better attack that recovers m in \mathcal{O}(\sqrt{B}) with high probability
- Can be the difference between 2^{80} and 2^{40}
Lemma: For appropriate \alpha \approx \frac{1}{2}, if m is a uniform n-bit integer then with high probability there exist r,s with 1 < r \le s \le 2^{\alpha n} for which m = r \cdot s
- Example: For n=64, with probability 0.35 there exist r,s with length at most 34 bits such that m = r \cdot s

Quadratic Improvement in Recovering Message (2/2)

Input: Public key \langle N, e \rangle; ciphertext c; bound 2^n
Output: m < 2^n such that m^e = c \bmod N \begin{align*} &\textbf{set } T \coloneqq 2^{\alpha n}\\ &\textbf{for } r = 1 \text{ to } T:\\ &\quad x_r \coloneqq [c/r^e \bmod N]\\ &\textbf{sort } \text{the pairs } \{(r,x_r)\}_{r=1}^T \text{ by } x_r\\ &\textbf{for } s = 1 \text{ to } T:\\ &\quad \textbf{if } [s^e \bmod N] \overset{?}{=} x_r \text{ for some } r\\ &\quad \quad \textbf{return } [r \cdot s \bmod N] \end{align*}

Encrypting Short Messages Using Small e

Suppose m < N^{1/e}
Raising m to the eth power involves no modular reduction
Give c, message m = c^{1/e} can be computed over the integers in \textsf{poly}(\| N \|) time
Suppose e = 3 and \| N \| = 2048 bits; then the attack works when m is a 256-bit string

Sending the Same Message to Multiple Receivers (1/2)

Suppose e = 3
Suppose the same message m is encrypted to three receivers having public keys pk_1 = \langle N_1, 3 \rangle, pk_2 = \langle N_2, 3 \rangle, pk_3 = \langle N_3, 3 \rangle
Assume \gcd(N_i, N_j) = 1 for i \neq j

Sending the Same Message to Multiple Receivers (2/2)

Eavesdropper observes c_1 = [m^3 \bmod N_1], c_2 = [m^3 \bmod N_2], c_3 = [m^3 \bmod N_3]
For N^* = N_1N_2N_3, by CRT there exists a unique \hat{c} < N^* such that \hat{c} =c_1 \bmod N_1\\ \hat{c} = c_2 \bmod N_2\\\hat{c} = c_3 \bmod N_3
As m < \min\{N_1, N_2, N_3\}, we have m^3 < N^*
Then \hat{c} = m^3 over the integers
Message m can be recovered by computing the integer cube root of \hat{c}

RSA Keys Should be Chosen Carefully

Suppose all employees in a company share the same RSA modulus N
Suppose two employees have encryption exponents e_1, e_2 such that e_1 \neq e_2 and \gcd(e_1, e_2) = 1
Suppose the same message m is encrypted to give c_1 = m^{e_1} \bmod N \text{ and } c_2 = m^{e_2} \bmod N
Then m can be recovered

RSA-OAEP

OAEP = Optimal Asymmetric Encryption Padding
CCA-secure encryption scheme from RSA
RSA-OAEP has been standardized (see RFC 8017)

RSA-OAEP

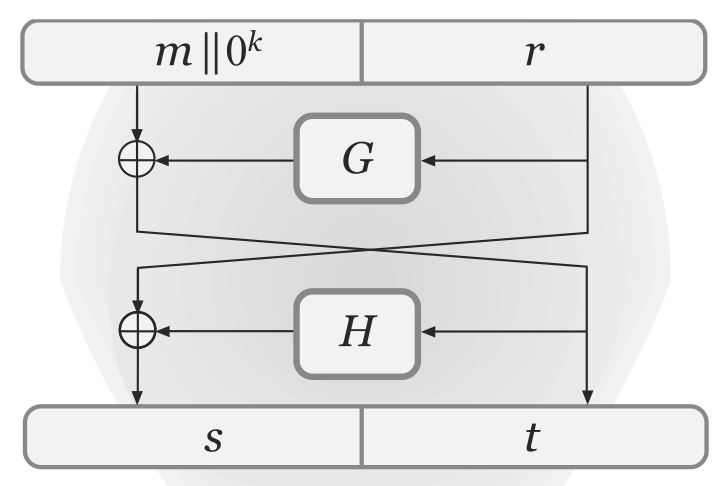
Let l, k \in \mathbb{N} such that 2k+l < \| N \|
Suppose a message m \in \{0,1\}^l is to be encrypted
It is mapped to a message \hat{m} \in \{0,1\}^{2k+l}
\hat{m} is encrypted using plain RSA
Let G: \{0,1\}^k \mapsto \{0,1\}^{l+k} and H: \{0,1\}^{l+k} \mapsto \{0,1\}^k be hash functions
Let m' = m \| 0^k and choose r uniformly from \{0,1\}^k
\hat{m} = s \| t where t = m' \oplus G(r) and s = r \oplus H(t)

RSA-OAEP

\hat{m} = s \| t where t = m' \oplus G(r) and s = r \oplus H(t)
RSA ciphertext is set to c = \hat{m}^e \bmod N
To decrypt c, first obtain \hat{m} as c^d \bmod N
To get m from \hat{m}, compute r = H(t) \oplus s \text{ and } m'= G(r) \oplus t

Public-Key Encryption

Public-Key Encryption Workflow

Why bother with private-key encryption?

Public-Key Encryption Schemes

CPA Security

Eavesdropping Indistinguishability Experiment

Security Definition

CPA-Security for Public-Key Encryption

El Gamal Encryption (1/2)

El Gamal Encryption (2/2)

CPA-Security of El Gamal Encryption

CPA-Security of El Gamal Encryption

CPA-Security of El Gamal Encryption

CPA-Security of El Gamal Encryption

CPA-Security of El Gamal Encryption

Multiple Encryptions

Defining CPA-Security for Multiple Encryptions

The Left-or-Right Oracle

LR-Oracle Experiment

Security Definition

CPA-Security \implies Indistinguishable Multiple Encryptions

Proof (1/7)

Proof (2/7)

Proof (3/7)

Proof (4/7)

Proof (5/7)

Proof (6/7)

Proof (7/7)

Plain RSA

Plain RSA Key Generation

Plain RSA Encryption and Decryption

The RSA Experiment

The RSA Assumption

Attacks on Plain RSA

Quadratic Improvement in Recovering Message (1/2)

Quadratic Improvement in Recovering Message (2/2)

Encrypting Short Messages Using Small e

Encrypting Related Messages

Sending the Same Message to Multiple Receivers (1/2)

Sending the Same Message to Multiple Receivers (2/2)

RSA Keys Should be Chosen Carefully

RSA-OAEP

RSA-OAEP

RSA-OAEP

Further Reading