Faster Food Deliveries using ZK Proofs

Saravanan Vijayakumaran

October 4, 2023

The Problem

Food delivery agents stop at the IITB main gate to enter name and phone number
- Food gets cold 😠
Why not have the data on a QR code?
- No guarantees about the correctness of the data
What if a trusted party verified the data and signed it?
- The Aadhaar infrastructure (almost) does what we want
The Aadhaar Offline eKYC document is a digitally signed document containing the card holder’s details

Getting the Offline eKYC Document

Find Offline eKYC Download Link

Set 4-Digit PIN

Success Screen

Cryptographic Hash Functions

Methods for deterministically mapping a long input string to a shorter output called a digest
Primary requirement is that it should be infeasible to find collisions, i.e. two distinct inputs having same digest

Non-Cryptographic Hash Functions

Used to build hash tables — key-value stores with faster lookup time

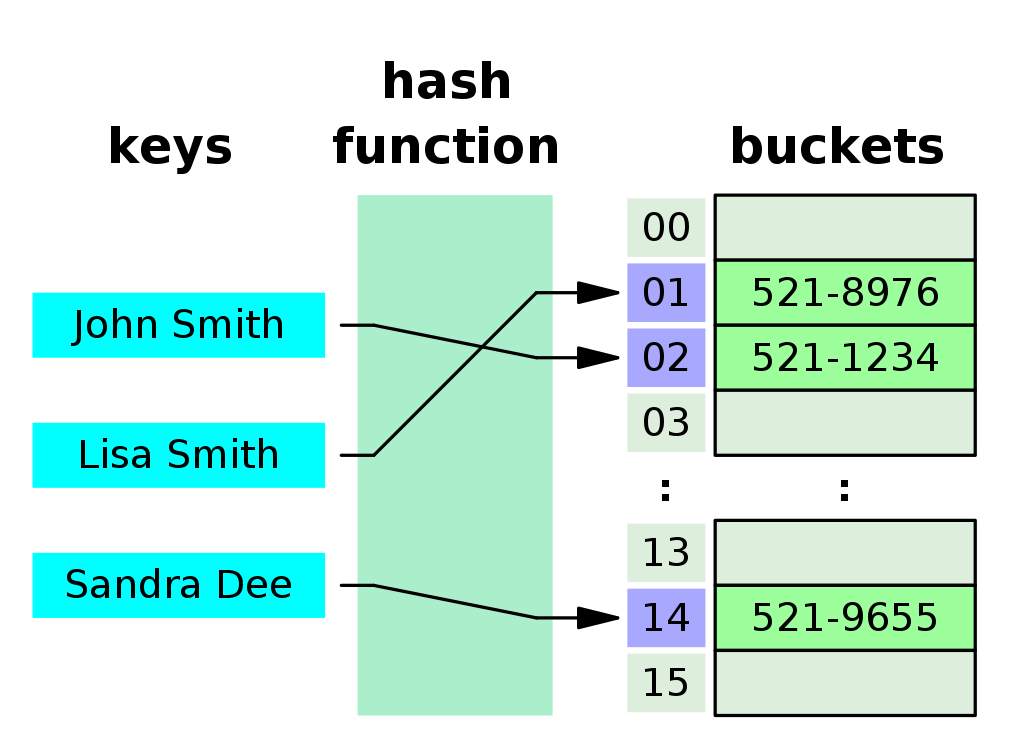
Image credit: Jorge Stolfi

Handling Collisions in Hash Tables

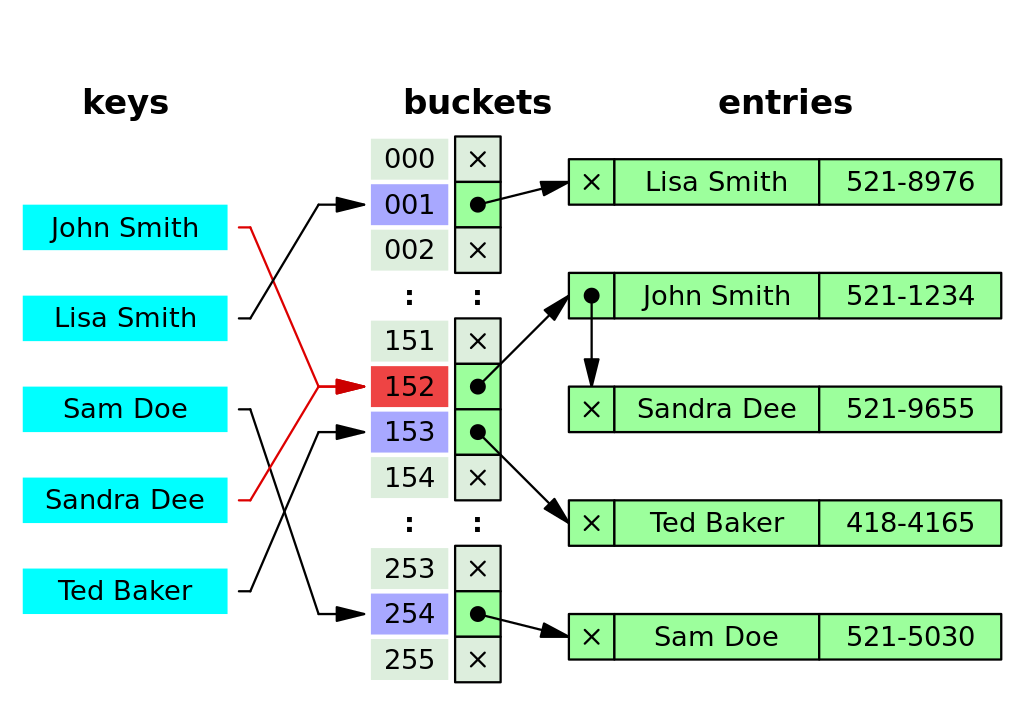
Image credit: Jorge Stolfi

Collision Avoidance

A collision is said to occur if \(h(x) = h(x')\) for \(x \neq x'\)
For non-cryptographic hash functions, the goal is to minimize collisions
For cryptographic hash functions, the goal is to completely avoid collisions
- Achieved by defining a large co-domain for \(h\)

Co-Domain for 256-bit Output Length

SHA-256

SHA = Secure Hash Algorithm, 256-bit output length
Accepts bit strings of length upto \(2^{64}-1\)
Announced in 2001 by NIST

Two Stages

Output calculation has two stages
- Preprocessing
- Hash Computation

Preprocessing

The input \(M\) is padded to a multiple of 512 bits
A 256-bit state variable \(H^{(0)}\) is set to \[\begin{align*} \begin{split} H_0^{(0)} = \texttt{0x6A09E667},& \quad H_1^{(0)} = \texttt{0xBB67AE85},\\ H_2^{(0)} = \texttt{0x3C6EF372},& \quad H_3^{(0)} = \texttt{0xA54FF53A},\\ H_4^{(0)} = \texttt{0x510E527F},& \quad H_5^{(0)} = \texttt{0x9B05688C},\\ H_6^{(0)} = \texttt{0x1F83D9AB},& \quad H_7^{(0)} = \texttt{0x5BE0CD19}. \end{split} \end{align*}\]
First 32 bits in the fractional parts of the square roots of the first eight primes
NUMS = Nothing Up My Sleeve

Hash Computation

A function \(f: \{0,1\}^{512} \times \{0,1\}^{256} \rightarrow \{0,1\}^{256}\) is used. It is called the compression function
Padded input is split into 512-bit blocks \(M^{(1)}, \ldots, M^{(N)}\)
Given \(H^{(i-1)}\), the next \(H^{(i)}\) is calculated as \[\begin{equation*} H^{(i)} = f(M^{(i)}, H^{(i-1)}), \quad 1 \le i \le N. \end{equation*}\]
\(H^{(N)}\) is the output of SHA-256 for input \(M\)

Building Blocks of \(f\)

\(U\), \(V\), \(W\) are 32-bit words
\(U \land V, U \lor V\), \(U \oplus V\) denote bitwise AND, OR, XOR
\(U + V\) denotes integer sum modulo \(2^{32}\)
\(\lnot U\) denotes bitwise complement
For \(1 \le n \le 32\), the shift right and rotate right operations \[\begin{align*} \textsf{SHR}^n(U) & = \underbrace{000 \cdots 000}_{n \textrm{ zeros}} u_0 u_1 \cdots u_{30-n} u_{31-n}, \\ \textsf{ROTR}^n(U) & = u_{31-n+1} u_{31-n+2} \cdots u_{30} u_{31} u_0 u_1 \cdots u_{30-n} u_{31-n}, \end{align*}\]

Building Blocks of \(f\)

Bitwise choice and majority functions \[\begin{align*} \textsf{Ch}(U,V,W) & = (U \land V) \oplus (\lnot U \land W), \\ \textsf{Maj}(U,V,W) & = (U \land V) \oplus (U \land W) \oplus (V \land W), \end{align*}\]
Let \[\begin{align*} \Sigma_0(U) & = \textsf{ROTR}^{2}(U) \oplus \textsf{ROTR}^{13}(U) \oplus \textsf{ROTR}^{22}(U) \\ \Sigma_1(U) & = \textsf{ROTR}^{6}(U) \oplus \textsf{ROTR}^{11}(U) \oplus \textsf{ROTR}^{25}(U) \\ \sigma_0(U) & = \textsf{ROTR}^{7}(U) \oplus \textsf{ROTR}^{18}(U) \oplus \textsf{SHR}^{3}(U) \\ \sigma_1(U) & = \textsf{ROTR}^{17}(U) \oplus \textsf{ROTR}^{19}(U) \oplus \textsf{SHR}^{10}(U) \end{align*}\]

\(f\) Calculation

Maintains internal state of 64 words \[\{W_j \mid j = 0,1,\ldots,63\}\]
Uses 64 constant words \(K_0, K_1, \ldots, K_{63}\) derived from the first 64 primes
\(f(M^{(i)}, H^{(i-1)})\) proceeds as follows
1. Internal state initialization \[\begin{equation*} W_j = \begin{cases} M_j^{(i)} & 0 \le j \le 15, \\ \sigma_1(W_{j-2}) + W_{j-7} + \sigma_0(W_{j-15}) + W_{j-16} & 16 \le j \le 63. \end{cases} \end{equation*}\]
2. Initialize eight 32-bit words \[\begin{equation*} (A,B,C,D,E,F,G,H) = \left(H_0^{(i-1)}, H_1^{(i-1)}, \ldots, H_6^{(i-1)}, H_7^{(i-1)}\right). \end{equation*}\]
3. For \(j = 0,1,\ldots,63\), iteratively update \(A,B,\ldots,H\) \[\begin{align*} \begin{split} & T_1 = H + \Sigma_1(E) + \textsf{Ch}(E,F,G) + K_j + W_j \\ & T_2 = \Sigma_0(A) + \textsf{Maj}(A,B,C) \\ & (A,B,C,D,E,F,G,H) = (T_1+T_2, A, B, C, D+T_1, E, F, G) \end{split} \end{align*}\]
4. Calculate \(H^{(i)}\) from \(H^{(i-1)}\) \[\begin{equation*} (H_0^{(i)}, H_1^{(i)}, \ldots, H_7^{(i)}) = \left(A+H_0^{(i-1)}, B+H_1^{(i-1)}, \ldots, H+H_7^{(i-1)}\right). \end{equation*}\]

Observations

SHA-256 is complicated but can be computed easily
Difficult to invert
Difficult to find collisions

Applications of Hash Functions

Password hashing
- Servers store hashes of passwords instead of actual passwords
Commitment Schemes
- To commit to a secret \(x\), publish \(H(\textsf{salt} \| x)\)
- To prove commitment to \(x\), reveal \(\textsf{salt}\)

Structure of the Offline eKYC Document

XML Format

<?xml version="1.0" encoding="UTF-8"?>
<note>
  <to>eeseminar</to>
  <from>Sibi</from>
  <heading>Reminder</heading>
  <body>We have a colloquium today. Please attend!</body>
</note>

XML = eXtensible Markup Language
Textual data format for representing arbitrary data

Base64

Binary-to-text encoding used to represent some fields in the XML file
Divides a byte sequence into groups of 3 bytes (24 bits)
- Adds padding if necessary
Divides a 24 bit chunk into four 6 bit chunks
Maps each 6 bit chunk to a character from
- ABCDE...XYZ
- abcde...xyz
- 0123456789
- +
- /

Contents of Offline eKYC Document

<?xml version="1.0" encoding="UTF-8"?>
<OfflinePaperlessKyc referenceId="372520231003155749167">
  <UidData>
    <Poi dob="DD-MM-YYYY"
      e="558d55fe5740c50058...518b702521b1448a6509ccb"
      gender="M"
      m="328f6d1c0adad4ad4...cf3589b98c617aa1d45afcf2"
      name="Saravanan Vijayakumaran"
    />
    <Poa careof="S/O XXXXXXXXXXXXX XXXXXXXXX"
         country="India"
         dist="Mumbai"
         house="EE122B, Dept of Electrical Engineering"
         landmark=""
         loc="Powai"
         pc="400076"
         po="Powai IIT"
         state="Maharashtra"
         street="I.I.T.Bombay"
         subdist="Mumbai"
         vtc="Mumbai"
    />
    <Pht> ..snip.. </Pht>
  </UidData>
  <Signature xmlns="http://www.w3.org/2000/09/xmldsig#">
  <SignedInfo>
    <CanonicalizationMethod Algorithm="<snip>"/>
    <SignatureMethod Algorithm="<snip>#rsa-sha1"/>
    <Reference URI="">
      <Transforms>
        <Transform Algorithm="<snip>"/>
      </Transforms>
      <DigestMethod Algorithm="<snip>#sha256"/>
      <DigestValue>rtb44DBF...TVVmMDWLZriVY=</DigestValue>
    </Reference>
  </SignedInfo>
  <SignatureValue>
    <snip>
  </SignatureValue>
  <KeyInfo>
    <snip>
  </KeyInfo>
</Signature>
</OfflinePaperlessKyc>

1: XML version
2: 4 digits of Aadhaar + timestamp
3: Start of user data
4: dob is the date of birth
5: Hash of email address
6: Hash of phone number
7: Photo encoded in base64 format
8: End of user data
9: Start of signature data
10: Start of data that is signed
11: Signature method is RSA-SHA1
12: Message digest generation method is SHA256
13: SHA256 hash of user data in base64 format
14: RSA signature verifiable by Aadhaar public key
15: Info about Aadhaar public key
16: End of signature data

Offline eKYC Document Generation

Hashes of user email/mobile number are generated and inserted into the rest of the user data
The user data is hashed using SHA256

The SHA256 hash is inserted into the following XML block

<SignedInfo>
  .
  .
  <DigestValue>SHA256 hash</DigestValue>
  .
  .
</SignedInfo>

The SignedInfo block is hashed with SHA1 and signed with Aadhaar’s private key
Any change to the user data will invalidate the signature

Offline eKYC Workflow

sequenceDiagram
  participant Alice
  participant Bank
  Alice->>Bank: Hello Bank, here is my eKYC zip file?
  Bank->>Alice: What's the four digit code?
  Alice->>Bank: It is 0076
  Note right of Bank: Unzips file and checks RSA signature.<br/> Checks photo matches Alice's appearance
  Bank->>Alice: What's your mobile number?
  Alice->>Bank: It is 9833456789
  Note right of Bank: Calculates hash of number and<br/> checks equality with hash <br/> in document
  Bank->>Alice: What's your email address?
  Alice->>Bank: It is alice@gmail.com
  Note right of Bank: Calculates hash of email and<br/> checks equality with hash <br/> in document
  Bank->>Alice: Your eKYC is done!

Back to Faster Food Deliveries

Desired Workflow

sequenceDiagram
  participant Agent as Delivery Agent
  participant Guard as IITB Security
  Agent->>Guard: Hello, here is SHA256 hash of my details?
  Guard->>Agent: Give me the RSA signature that <br/> authenticates this hash?
  Agent->>Guard: Here it is.
  Note right of Guard: Checks RSA signature
  Guard->>Agent: What's your name and mobile number?
  Agent->>Guard: Alice, 9833456789
  Guard->>Agent: Give me a proof that these are in the <br/> SHA256 hash you shared earlier
  Agent->>Guard: Here it is.
  Note right of Guard: Verifies the proof
  Guard->>Agent: You can enter campus.

How to generate the proof?

We want to prove that the name and phone number are contained in the preimage of a SHA256 hash
- Without revealing the other bytes in the preimage
Zero-Knowledge Proofs
- Cryptographic techniques for proving a statement without revealing nothing else
SNARK = Succinct Non-interactive Arguments of Knowledge
- Enables verifiable computation
zkSNARK = Zero-Knowledge SNARK
- Additionally, enables privacy

Statement Representation

To prove statements using zkSNARKs, they need to be expressed as arithmetic circuits
- Circuit variables are prime field elements
- Only addition and multiplication are allowed
Prime fields
- \(\mathbb{F}_p = \{0,1,\ldots,p-1\}\) where \(p\) is a prime
- Arithmetic modulo \(p\)

Arithmetic Circuit Example

flowchart LR
  a[a] --> plus1(+)
  b[b] --> plus1
  c[c] --> mul1(*)
  d[d] --> mul1
  plus1 --> plus2(+)
  mul1 --> plus2
  plus2 --> e[e]
  a --> mul2(*)
  e[e] --> mul2
  mul2 --> f[f]

Rank-1 Constraint Systems

Statement is represented using quadratic constraints of the form \[\begin{align*} \left(a_0 + \sum_{i=1}^n a_i w_i \right) \cdot \left(b_0 + \sum_{i=1}^n b_i w_i\right) = \left( c_0 + \sum_{i=1}^n c_i w_i\right) \end{align*}\]
The \(a_i, b_i, c_i\) values are determined by the statement
The \(w_i\)’s are witness values specific to the instance

Rank 1?

\[\begin{align*} & \left(a_0 + \sum_{i=1}^n a_i w_i \right) \cdot \left(b_0 + \sum_{i=1}^n b_i w_i\right) \\ = & \langle \textbf{a}, (1,\textbf{w}) \rangle \cdot \langle \textbf{b}, (1,\textbf{w}) \rangle \\ = & \begin{bmatrix} 1 & \textbf{w} \end{bmatrix} \underbrace{\begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix} \begin{bmatrix} b_0 & b_1 & \cdots & b_n \end{bmatrix}}_{A} \begin{bmatrix} 1 \\ \textbf{w}^T \end{bmatrix} \end{align*}\]

R1CS for SHA256

SHA256 has operations like
- Bitwise AND, OR, XOR, complement
- Choice function
- Integer sum mod \(2^{32}\)
- Shift right and rotate right
How can these be represented in a R1CS?

R1CS Gadgets for SHA256

AND and OR Gates

If \(a \in \mathbb{F}_p = \{0,1,\ldots,p-1\}\) satisfies \(a(1-a) = 0\), then \(a \in \{0,1\}\)
Given \(a(1-a) = 0, b(1-b) = 0\)
- \(c = a \land b\) is expressed as \[ab = c\]
- \(c = a \lor b\) is expressed as \[(1-a)\cdot(1-b) =1- c\]

XOR Gate

Given \(a(1-a) = 0, b(1-b) = 0\), we can express \(c = a \oplus b\) as \[(a+a) \cdot b = a + b - c.\]
If \(b=0\), then \(c = a\)
If \(b=1\), then \(c = 1-a\)

Addition Modulo \(2^{32}\)

A 32-bit word = Vector of 32 booleans
- \(U = [U_0, U_1, \ldots, U_{31}]\)
- Costs 32 constraints of the form \(x(1-x) = 0\)
To get \(W = U +V \bmod 2^{32}\)
- Calculate field element \(u = \sum_{i=0}^{31} U_i \cdot 2^i\)
- Calculate field element \(v = \sum_{i=0}^{31} V_i \cdot 2^i\)
- Allocate 33 bits \(W = [W_0, W_1,\ldots,W_{32}]\)
- Calculate field element \(w = \sum_{i=0}^{32} W_i \cdot 2^i\)
- Check that \(w = u+v\)
- Truncate \(W\) to 32 bits

Selective Disclosure of SHA256 Preimages

Agent will reveal two SHA256 hashes \(h_1\), \(h_2\)
The first hash \(h_1\) has been signed by Aadhaar system
Agent will prove knowledge of message \(\vec{m} \in \{0,1\}^n\) and mask vector \(\vec{v} \in \{0,1\}^n\) such that \[\begin{align*} & \text{SHA256}(\vec{m}) = h_1, \\ & \text{SHA256}(\vec{m} \circ \vec{v}) = h_2. \\ \end{align*}\]
Agent will reveal \(\vec{m} \circ \vec{v}\)
Guard can verify that the hash of \(\vec{m} \circ \vec{v}\) matches \(h_2\)

Proof Generation Time

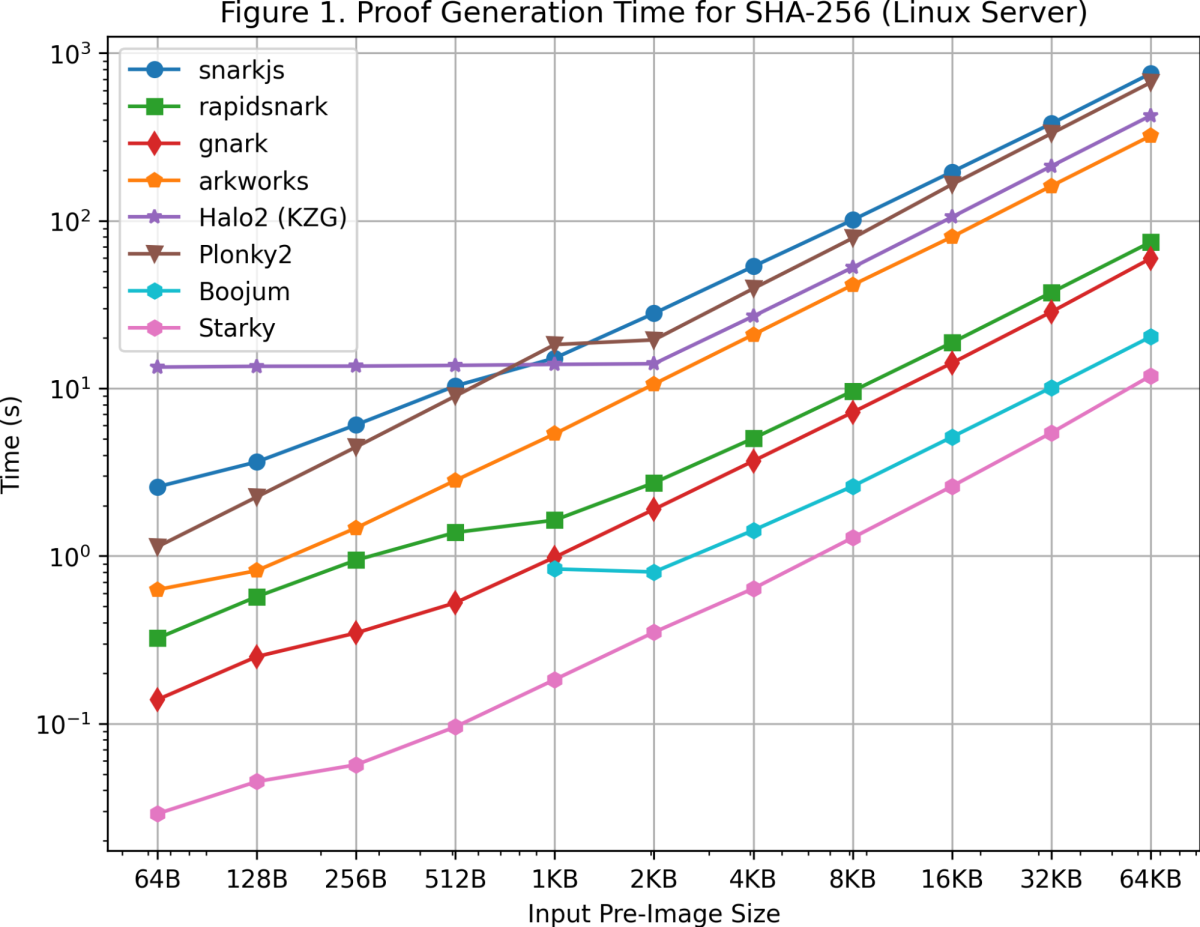
Image credit: Celer Network Benchmarks

Prover Memory Requirement

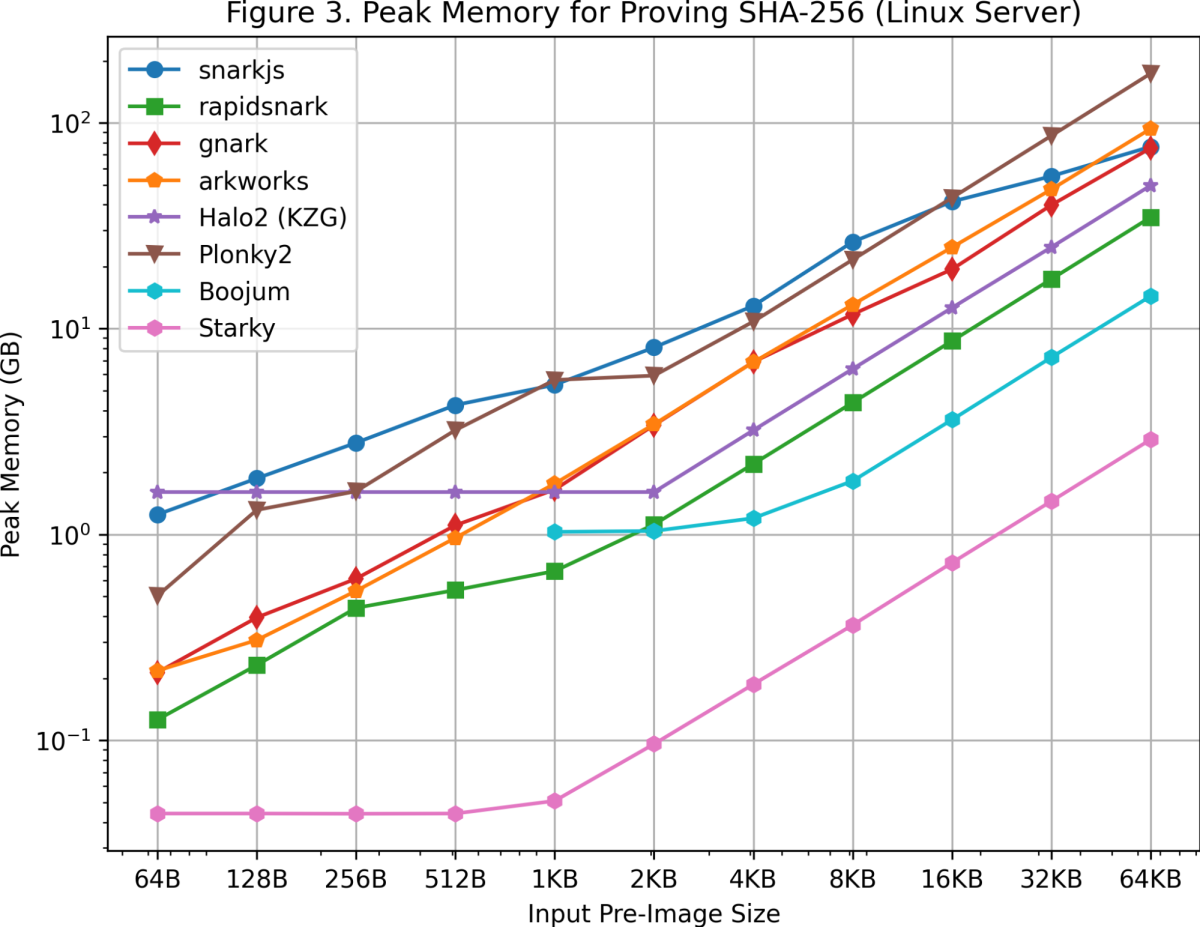
Image credit: Celer Network Benchmarks

Nova

A recursive SNARK for incremental verifiable computation
Allows a prover to prove that for some function \(F\) and public values \(z_0\) and \(z_n\), it knows private \(w_{i}\)’s such that \[z_n = F \left( \ldots F \left(F \left(F \left( z_0, w_0 \right), w_1 \right),w_2\right), \ldots,w_{n-1}\right).\]
Nova is a folding scheme which folds all the R1CS steps into a single relaxed R1CS instance
- The number of constraints in the latter is proportional to the number of constraints in a single step

Selective Disclosure of SHA256 Preimages using Nova

SHA256 hash computation has an iterative structure
Our Nova step function \(F\) is specified as follows
- Private inputs are message and mask blocks
- Public outputs are digests of message and masked message
- Number of steps is \(N\)

Demo

Resources

Aadhaar eKYC Documentation https://uidai.gov.in/en/ecosystem/authentication-devices-documents/about-aadhaar-paperless-offline-e-kyc.html
Nova reference implementation https://github.com/microsoft/Nova
Nova-SHA256 repo https://github.com/avras/nova-sha256
Celer Network Benchmarks https://blog.celer.network/
Nova-Aadhaar repo (coming soon..)

Faster Food Deliveries using ZK Proofs

The Problem

Getting the Offline eKYC Document

Login to myAadhaar

Find Offline eKYC Download Link

Set 4-Digit PIN

Success Screen

Cryptographic Hash Functions

Non-Cryptographic Hash Functions

Handling Collisions in Hash Tables

Collision Avoidance

Co-Domain for 256-bit Output Length

SHA-256

Two Stages

Preprocessing

Hash Computation

Building Blocks of \(f\)

Building Blocks of \(f\)

\(f\) Calculation

Observations

Applications of Hash Functions

Structure of the Offline eKYC Document

XML Format

Base64

Contents of Offline eKYC Document

Offline eKYC Document Generation

Offline eKYC Workflow

Back to Faster Food Deliveries

Desired Workflow

How to generate the proof?

Statement Representation

Arithmetic Circuit Example

Rank-1 Constraint Systems

Rank 1?

R1CS for SHA256

R1CS Gadgets for SHA256

AND and OR Gates

XOR Gate

Addition Modulo \(2^{32}\)

Selective Disclosure of SHA256 Preimages

Selective Disclosure of SHA256 Preimages

Proof Generation Time

Prover Memory Requirement

Nova

Selective Disclosure of SHA256 Preimages using Nova

Demo

Resources