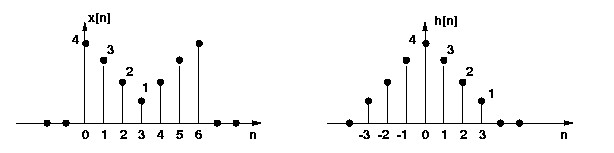
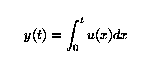Problem 1: Given two sequences x[n] and h[n]
as shown in the figure below.
|
(i)
|
Convolve x[n] and h[n] without using matlab routines.
|
|
(ii)
|
If X[k] and H[k] are DFTs of x[n] and h[n] respectively, find a sequence
x1[n] such that X1[k] = X[k]H[k] (Hint: This is circular convolution)
|
|
(iii)
|
Use Matlab routines to carry out convolution. Try doing circular
convolution.
|
|
(iv)
|
Use circular convolution to implement linear convolution.
|
|
(v)
|
Now deconvolve two signals.
That is given x[n], h[n] and y[n] = x[n]*h[n], recover x[n] from y[n]
and h[n].
|
Problem 2: Do the following.
|
(i)
|
Plot triangular, sawtooth and square waveforms using matlab routines.
|
|
(ii)
|
Modulate a sine wave using triangular and sawtooth waveforms. Do this
using different frequencies. Do this for amplitude as well as frequency
modulation.
|
|
(iii)
|
Now demodulate each of the modulated signals.
|
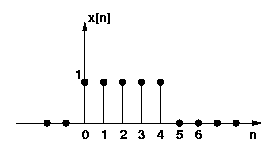
Problem 3: Given a sequence x[n] as shown in the figure below
|
(i)
|
Generate DFT matrix for 10-point DFT.
|
|
(ii)
|
Now using matrix multiplication find the DFT of the sequence x[n].
|
|
(iii)
|
Find the inverse DFT again using matrices.
|
|
(iv)
|
Pad 11 zeros at the end of the sequence x[n]. Now compute the DFT of
sequence x[n] using matlab FFT routine.
|
|
(v)
|
Replace x[n] by cos[(PI/20)*n]. Find the spectrum. Is it a delta function?
If not generate
y[n] = (x[n]).(cosine window)
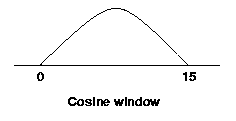
Find the spectrum of y[n]. How is this related to that of x[n]?
|
Problem 4: Consider the integration of a
function
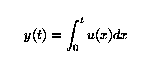
|
(i)
|
Numerically this can be achieved using 3/8 rule of integration
y(n+2) = y(n-1) + (3/8)[u(n+2) + 3u(n+1) + 3u(n) +
u(n-1)]
Take a few non-trivial continuous functions and integrate them
numerically. Compare the results with those obtained analytically. Vary
the sampling rate and interprete the results.
|
|
(ii)
|
Use trepizoidal rule and compare the results.
|
|
(iii)
|
Repeat the same problem if, instead of integration, one wishes to carry
out differentiation, ie, when one writes
x(n) = u(n) - u(n-1)
How is this different from the actual value of dx/dt? After having
integrated the function u(x) using 3/8 rule of integration, if you
differentiate it do you get back the original function?
|
|
(iv)
|
Analyze your results in frequency domain.
|
|