Cryptographic Hardness Assumptions

Saravanan Vijayakumaran

Department of Electrical Engineering, IIT Bombay

October 9, 2024

The Factoring Problem

  • Given a composite integer N, the factoring problem is to find integers p,q >1 such that pq = N

  • Can be solved in exponential time

    • Trial division runs in \mathcal{O}\left( \sqrt{N} \cdot \textsf{polylog}(N) \right) time

  • No polynomial-time algorithm is known for factoring

Generating Hard Instances of the Factoring Problem

  • Instance = An integer N which needs to be factored
  • Picking random n-bit integers x_1, x_2 and giving N = x_1 x_2 can result in easy instances
  • Instead, pick a pair of random n-bit primes p,q and output their product N = pq
  • How can we generate random primes?

Generating Random Primes

  • Algorithm for generating an n-bit prime

  • Input: Length n, loop count t

  • Output: A uniform n-bit prime \begin{align*} & \textbf{for } i=1 \text{ to } t:\\ &\quad p' \leftarrow \{0,1\}^{n-1}\\ &\quad p \coloneqq 1 || p' \\ &\quad \textbf{if } p \text{ is prime } \textbf{return } p\\ &\textbf{return } \textsf{fail} \end{align*}

  • We need to clarify two points

    • The probability that a uniform n-bit integer is a prime
    • How can we efficiently check whether a given integer is a prime?

Distribution of Primes

  • Theorem: For any n > 1, the fraction of n-bit integers that are prime is at least \frac{1}{3n}

  • Set the loop count t = 3n^2

  • The probability that a prime is not chosen in all t iterations is at most \left(1-\frac{1}{3n}\right)^t \leq e^{-n}

Primality Testing

Primality Testing

  • First efficient algorithms were developed in the 70s

  • Probabilistic algorithms with following guarantees

    • If input p is a prime, the algorithms always output “prime”
    • If p is composite, the algorithms might output “prime” with a negligible probability

  • A deterministic polynomial-time algorithm was found in 2002 by Agrawal, Kayal, Saxena (AKS)

    • Not used in practice due to slower running time

Group Exponentiation

  • Computing a^b \bmod N for a \in \mathbb{Z}_N and exponent b can be done in \mathcal{O}(\| b \| \times \|N\|^2) time
  • The square and multiply algorithm \begin{align*} & x \leftarrow a, t \leftarrow 1 \\ & \textbf{while } b > 0\\ & \quad \textbf{if } b \text{ is odd}\\ &\quad \quad t \leftarrow t \cdot x \bmod N, \quad b \leftarrow b-1\\ & \quad \textbf{end if }\\ & \quad x \leftarrow x^2 \bmod N, \quad b \leftarrow b/2\\ & \textbf{return } t \end{align*}

A Primality Test Based on FLT

  • Fermat’s little theorem: If p is a prime and a is any integer not divisible by p, then a^{p-1} = 1 \bmod p.

  • The Primality Test

    • Choose a random integer a from \{1,2,3,\ldots,N-1\}
    • Compute a^{N-1} \bmod N
    • If a^{N-1} \neq 1 \bmod N, then N is not a prime

  • If a^{N-1} = 1 \bmod N, we get no information about the primality of N

Everything in \left(\mathbb{Z}_N^* \right)^c Proves that N is Composite

  • Suppose a \in \{1,2,\ldots,N-1\} and a \notin \mathbb{Z}_N^*

    • \gcd(a, N) \neq 1 implies \gcd(a^{N-1}, N) \neq 1
    • Then a^{N-1} \neq 1 \bmod N
    • Such an a proves that N is composite

\left(\mathbb{Z}_N^* \right)^c is a Small Set

  • Integers in \{1,\ldots,N-1\} not belonging to \mathbb{Z}_N^* are rare

  • If N is prime, then there are no such integers

  • For composite N = p_1^{e_1} \cdots p_k^{e_k}, we have |\mathbb{Z}_N^*| =\phi(N) =\prod_i p_i^{e_i-1}(p_i-1)

  • If p_1,p_2,\ldots,p_k are large primes, then the fraction of \{1,2,\ldots,N-1\} in \mathbb{Z}_N^* is close to 1

Witnesses for Compositeness in \mathbb{Z}_N^*

  • We say that an integer a \in \mathbb{Z}_N^* is a witness for compositeness of N if a^{N-1} \neq 1 \bmod N

  • \gcd(a, N) = 1 \implies \gcd(a^{N-1}, N) = 1

    • Xa^{N-1} + YN =1 for some integers X,Y
    • So Xa^{N-1} = 1 \bmod N
    • But a^{N-1} \bmod N may or may not be equal to 1

  • So the a’s in \mathbb{Z}_N^* may or may not be witnesses

Testing Primality When At Least One Witness Exists

  • Theorem If there exists a witness in \mathbb{Z}_N^* that N is composite, then at least half the elements of \mathbb{Z}_N^* are witnesses that N is composite

  • If a witness exists, the following primality test fails to detect the compositeness of N with probability at most 2^{-t}

    1. For i=1,2,\ldots,t, repeat steps 2 and 3.
    2. Pick a uniformly from \{1,2,\ldots,N-1\}.
    3. If a^{N-1} \neq 1 \bmod N, return “composite’”
    4. If all t iterations have a^{N-1} = 1 \bmod N, return “prime”

Number of Witnesses When At Least One Witness Exists

  • Theorem: Suppose there exists a witness that N is composite. Then at least half the elements of \mathbb{Z}_N^* are witnesses that N is composite.

  • Proof

    • Let \textsf{Bad} be the subset of \mathbb{Z}_N^* that are not witnesses
    • \textsf{Bad} is a subgroup of \mathbb{Z}_N^*
    • By the hypothesis, it is a strict subgroup of \mathbb{Z}_N^*
    • By Lagrange’s theorem, |\textsf{Bad}| \le |\mathbb{Z}_N^*|/2
    • So |\textsf{Bad}^c| \ge |\mathbb{Z}_N^*|/2

Carmichael Numbers

  • Composite numbers for which a^{N-1} = 1 \bmod N for all integers a \in \mathbb{Z}_N^*
  • There are infinitely many Carmichael numbers
  • Example: 561= 3 \cdot 11 \cdot 17
  • We cannot rely on the existence of at least one witness in constructing our primality test

Square Roots of Unity Modulo a Prime

  • We say that x \in \mathbb{Z}_N^* is a square root of 1 modulo N if x^2 = 1 \bmod N.

  • Lemma: If N is an odd prime, then the only square roots of 1 modulo N are \pm 1 \bmod N.

The Sequence of Square Roots of Unity Modulo an Odd Prime

  • For an odd prime N, we have N-1 = 2^r u where r \ge 1 and u is odd

  • Suppose a^{N-1} = a^{2^ru} = 1 \bmod N

  • Consider the sequence a^u \bmod N,a^{2u} \bmod N, \ldots, a^{2^r u} \bmod N

  • It can only be in one of the following forms

    • 1,1,1,1,\ldots,1
    • -1,1,1,\ldots,1
    • \star,\star,\ldots,\star,-1,1,1,\ldots,1

  • For an odd integer N, if we do not observe this sequence then N is composite

The Sequence of Square Roots of Unity Modulo an Odd Prime

  • In other words, when N is an odd prime, the sequence a^u \bmod N,a^{2u} \bmod N, \ldots, a^{2^r u} \bmod N satisfies the following conditions

    • Either a^u = 1 \bmod N
    • Or one of a^u \bmod N, a^{2u} \bmod N,\ a^{2^2 u} \bmod N,\ \dots,\ a^{2^{r-1} u} \bmod N is equal to -1.

Strong Witnesses

  • We say that a \in \mathbb{Z}_N^* is a strong witness that N is composite if

    • a^u \neq 1 \bmod N and

    • a^{2^i u} \neq -1 \bmod N for all i \in \{0,1,2,\ldots,r-1\}.

  • If we can find even one strong witness, we can conclude that N is composite.

  • Theorem Let N be an odd number that is not a prime power. Then at least half the elements of \mathbb{Z}_N^* are strong witnesses that N is composite.

    • A prime power is of the form p^r where p is a prime and r \ge 1

Strategy for Proving Strong Witness Count

  • Let \textsf{Bad} \subseteq \mathbb{Z}_N^* be the set of elements that are not strong witnesses

  • We can define a set \textsf{Bad}' such that

    • \textsf{Bad} \subseteq \textsf{Bad}'
    • \textsf{Bad}' is a strict subgroup of \mathbb{Z}_N^*
    • By Lagrange’s theorem, |\textsf{Bad}| \le |\textsf{Bad}'| \le |\mathbb{Z}_N^*|/2
    • Hence, at least half of \mathbb{Z}_N^* are strong witnesses

  • See proof of Theorem 9.40 in Katz & Lindell

Defining \textsf{Bad}'

  • For N-1 = 2^r u, let i \in \{0,1,\ldots,r-1\} be the largest integer for which there exists an a \in \textsf{Bad} with a^{2^iu} = -1 \bmod N.
  • Since (-1)^u = -1 \bmod N, i is well-defined
  • Let \textsf{Bad}' = \{ a \in \mathbb{Z}_N^* \mid a^{2^iu} = \pm 1 \bmod N \}
  • \textsf{Bad}' is a subgroup of \mathbb{Z}_N^*

\textsf{Bad}' is a Strict Subgroup

  • \textsf{Bad}' = \{ a \in \mathbb{Z}_N^* \mid a^{2^iu} = \pm 1 \bmod N \}
  • Since N is an odd composite integer that is not a prime power, we have N = N_1 N_2 \text{ for } N_1, N_2 > 1 \text{ and } \gcd(N_1, N_2) = 1
  • By CRT, \mathbb{Z}_N^* \simeq \mathbb{Z}_{N_1}^* \times \mathbb{Z}_{N_2}^*
  • Let a \in \textsf{Bad}' be such that a^{2^i u} = -1 \bmod N
  • Let a \leftrightarrow (a_1, a_2), then a_1^{2^i u} = -1 \bmod N_1 \text{ and } a_2^{2^i u} = -1 \bmod N_2
  • Let b \in \mathbb{Z}_N^* such that b \leftrightarrow (a_1, 1). Then b^{2^i u} \leftrightarrow (a_1, 1)^{2^iu} = (-1,1) \not\leftrightarrow \pm 1
  • So b \not\in \textsf{Bad}' \implies \textsf{Bad}' \subsetneq \mathbb{Z}_N^*

Miller-Rabin Primality Test

  • Input: Odd integer N > 1 and parameter 1^t

  • Output: A decision as to whether N is prime or composite \begin{align*} & \text{{Compute $r \ge 1$ and odd $u$ such that $N-1 = 2^ru$}}\\ & \textbf{if } \text{$N$ is a perfect power, \textbf{return} ``composite''}\\ & \textbf{for } j=1 \text{ to } t:\\ &\quad a \leftarrow \{1,\ldots,N-1\}\\ &\quad \textbf{if } \text{$a^u \neq \pm 1 \bmod N$ and}\\ &\quad \quad \text{$a^{2^iu} \neq -1 \bmod N$ for $i \in \{1,\ldots,r-1\}$ } \\ &\quad \quad \text{\textbf{return} ``composite''}\\ &\quad \textbf{end if } \\ &\textbf{end for } \\ & \textbf{return } \text{``prime''} \end{align*}

The Factoring Assumption

The Factoring Experiment

  • Let \textsf{GenModulus} be a PPT algorithm that, on input 1^n, outputs (N,p,q) where N = pq, and p and q are n-bit primes except with probability negligible in n.

  • The factoring experiment \textsf{Factor}_{\mathcal{A}, \textsf{GenModulus}}(n):

    • Run \textsf{GenModulus}(1^n) to obtain (N,p,q).
    • \mathcal{A} is given N, and outputs p',q' > 1.
    • The output of the experiment is 1 if N = p'q', and 0 otherwise.

  • We use p', q' in the above experiment because it is possible that \textsf{GenModulus} returns composite integers p, q albeit with negligible probability

The Factoring Assumption

  • Definition: Factoring is hard relative to \textsf{GenModulus} if for all PPT algorithms \mathcal{A} there exists a negligible function \textsf{negl} such that \Pr[\textsf{Factor}_{\mathcal{A}, \textsf{GenModulus}}(n) = 1] \le \textsf{negl}(n).

  • The factoring assumption states that there exists a \textsf{GenModulus} relative to which factoring is hard.

RSA

Plain RSA

  • Let \textsf{GenRSA} be a PPT algorithm that on input 1^n, outputs a modulus N that is the product of two n-bit primes, along with integers e,d > 1 satisfying ed = 1 \bmod \phi(N)

  • Define a public-key encryption scheme as follows:

    • \textsf{Gen:} On input 1^n, run \textsf{GenRSA}(1^n) to obtain N, e, and d.
      • The public key is \langle N,e \rangle and the private key is \langle N,d \rangle
    • \textsf{Enc:} On input a public key pk = \langle N,e \rangle and message m \in \mathbb{Z}_N^*, compute the ciphertext c = m^e \bmod N.
    • \textsf{Dec:} On input a private key sk = \langle N, d \rangle and ciphertext c \in \mathbb{Z}_N^*, output \hat{m} = c^d \bmod N.

The RSA Experiment

  • \textsf{RSA-inv}_{\mathcal{A}, \textsf{GenRSA}}(n):

    • Run \textsf{GenRSA}(1^n) to obtain (N,e,d)
    • Choose a uniform y \in \mathbb{Z}_N^*
    • \mathcal{A} is given N,e,y, and outputs x \in \mathbb{Z}_N^*
    • The output of the experiment is 1 if x^e = y \bmod N, and 0 otherwise.

The RSA Assumption

  • Definition: The RSA problem is hard relative to \textsf{GenRSA} if for all PPT algorithms \mathcal{A} there exists a negligible function \textsf{negl} such that \Pr[\textsf{RSA-inv}_{\mathcal{A}, \textsf{GenRSA}}(n) = 1] \le \textsf{negl}(n).

  • The RSA assumption states that there exists a \textsf{GenRSA} relative to which the RSA problem is hard

  • The RSA assumption is a stronger assumption than the factoring assumption

Cyclic Groups

Cyclic Groups

  • Definition: Let G be a finite group. For g \in G, the subgroup generated by g is given by \langle g \rangle = \{g, g^2, \ldots \}.

  • Definition: Let G be a finite group. We call G a cyclic group if there exists a g \in G such that G = \langle g \rangle. Such a g is called a generator of G.

  • Examples

    • 1 is a generator of \mathbb{Z}_N for all N > 1
    • 3 and 5 are generators of \mathbb{Z}_7^*

Order of Elements in a Finite Group

  • Definition: Let G be a finite group and g \in G. The order of g is the smallest positive integer i for which g^i = 1.

  • Proposition: In a finite group G, the order of an element g equals the order of the subgroup \langle g \rangle.

  • Corollary: If G is a group of prime order p, then G is cyclic. Furthermore, all elements of G except the identity are generators of G.

    • In \mathbb{Z}_p, all the integers other than 0 are generators.

\mathbb{Z}_p^* is Cyclic for Prime p

  • Theorem: If p is a prime, then Z_p^* is a cyclic group of order p-1

  • Proof can be found in Prof. Forney’s notes

The Discrete-Logarithm Assumption

The Discrete Logarithm

  • If G is a cyclic group of order q with generator g, then we can write G = \{g^0, g^1, g^2,\ldots, g^{q-1}\} where g^0 = e
  • For every h \in G, there is a unique x \in \mathbb{Z}_q such that g^x = h
  • We call this x the discrete logarithm of h with respect to g and write x = \log_g h

The Discrete-Logarithm Experiment

  • Let \mathcal{G} denote a polynomial-time, cyclic group generation algorithm which outputs a group, its order, and a generator

  • The discrete-logarithm experiment \textsf{DLog}_{\mathcal{A},\mathcal{G}}(n)

    1. Run \mathcal{G}(1^n) to obtain (G,q,g), where G is a cyclic group of order q (with \| q \| = n), and g is a generator of G
    2. Choose a uniform h \in G
    3. \mathcal{A} is given G, q, g, h, and outputs x \in \mathbb{Z}_q
    4. The output of the experiment is 1 if g^x = h, and 0 otherwise

The Discrete-Logarithm Assumption

  • Definition: We say the discrete-logarithm problem is hard relative to \mathcal{G} if for all PPT algorithms \mathcal{A} there exists a negligible function \textsf{negl} such that \Pr[\textsf{DLog}_{\mathcal{A}, \mathcal{G}}(n) = 1] \le \textsf{negl}(n).

  • The discrete-logarithm assumption states that there exists a \mathcal{G} relative to which the discrete-logarithm problem is hard

    • We will see two examples of \mathcal{G} later

The Diffie-Hellman Assumptions

Diffie-Hellman Protocol

The Diffie-Hellman Problems

  • Related to the problem of computing discrete logarithms, but not known to be equivalent to it

  • Two important variants

    • Computational Diffie-Hellman (CDH) Problem
    • Decisional Diffie-Hellman (DDH) Problem

Computational Diffie-Hellman (CDH) Problem

  • Consider a cyclic group G with a generator g
  • Given h_1, h_2 \in G, define \textsf{DH}_g(h_1, h_2) = g^{\log_g h_1 \cdot \log_g h_2}
  • That is, if h_1 = g^{x_1} and h_2=g^{x_2} then \textsf{DH}_g(h_1, h_2) = g^{x_1\cdot x_2} = h_1^{x_2} = h_2^{x_1}

The CDH Experiment

  • Let \mathcal{G} denote a polynomial-time, cyclic group generation algorithm

  • The CDH experiment \textsf{CDH}_{\mathcal{A},\mathcal{G}}(n)

    1. Run \mathcal{G}(1^n) to obtain (G,q,g), where G is a cyclic group of order q (with \| q \| = n), and g is a generator of G
    2. Choose uniform x_1, x_2 \in \mathbb{Z}_q and compute h_1 = g^{x_1}, h_2 = g^{x_2}
    3. \mathcal{A} is given G, q, g, h_1, h_2, and outputs h \in G
    4. The output of the experiment is 1 if h = g^{x_1 x_2}, and 0 otherwise

The CDH Assumption

  • Definition: We say the CDH problem is hard relative to \mathcal{G} if for all PPT algorithms \mathcal{A} there exists a negligible function \textsf{negl} such that \Pr[\textsf{CDH}_{\mathcal{A}, \mathcal{G}}(n) = 1] \le \textsf{negl}(n).

  • The CDH assumption states that there exists a \mathcal{G} relative to which the CDH problem is hard

Relation between the DL and CDH Problems

  • If discrete logarithms are easy to calculate in a group, then the CDH is also easy
  • So the CDH assumption is a stronger assumption than the DL assumption

The DDH Assumption

  • Let \mathcal{G} denote a polynomial-time, cyclic group generation algorithm

  • Definition: We say the DDH problem is hard relative to \mathcal{G} if for all PPT algorithms \mathcal{A} there exists a negligible function \textsf{negl} such that \begin{align*} &\bigg| \Pr[\mathcal{A}(G,q,g,g^x,g^y,g^z) = 1] \\ &\ \ - \Pr[\mathcal{A}(G,q,g,g^x,g^y,g^{xy}) = 1]\bigg| \le \textsf{negl}(n)\end{align*} where x,y,z\in \mathbb{Z}_q are uniformly chosen

  • The DDH assumption states that there exists a \mathcal{G} relative to which the DDH problem is hard

Prime-Order Cyclic Groups

  • Cyclic groups of prime order are preferred because the DL problem is hardest in such groups

    • DL problem in a group of order q becomes easier if q has small prime factors

  • Finding generators in prime-order cyclic groups is trivial

  • Subgroups of \mathbb{Z}_p^* and elliptic curves are two sources of prime-order cyclic groups

Prime-Order Subgroups of \mathbb{Z}_p^*

Finding a Prime-Order Subgroup

  • Suppose we want to generate a subgroup of \mathbb{Z}_p^* whose order is an n-bit prime
  • First, find an n-bit prime q
  • Then for r \in \{1,2,\ldots\} check if rq+1 is a prime
  • If such an r is found, set p= rq+1. Then G = \{ h^r \bmod p \mid h \in \mathbb{Z}_p^*\} is a subgroup of \mathbb{Z}_p^* of order q.

Subgroup of rth Residues

  • Theorem: Let p=rq+1 with p,q prime. Then G = \{ h^r \bmod p \mid h \in \mathbb{Z}_p^*\} is a subgroup of \mathbb{Z}_p^* of order q.

  • Proof

    • The function f_r(g) = [g^r \bmod p] is an r-to-1 function in \mathbb{Z}_p^*
    • As |\mathbb{Z}_p^*| = p-1 = rq, we have |G| = q

Finding a Generator of the Subgroup

  • G = \{ h^r \bmod p \mid h \in \mathbb{Z}_p^*\}

  • A generator of the subgroup G can be found as follows

    1. For p = rq+1, choose a uniform h \in \mathbb{Z}_p^* \setminus \{1\}
    2. If h^q = 1, then h is a generator of G

How large should p,q be?

  • Let n = \| q \| and l = \|p\|

  • Two types of algorithms are known for computing discrete logarithms in order-q subgroups of \mathbb{Z}_p^*

    • First type runs in time \mathcal{O}(\sqrt{q}) = \mathcal{O}(2^{n/2})
    • Second type runs in time 2^{\mathcal{O}\left((\log p)^{1/3}\cdot (\log\log p)^{2/3} \right)} = 2^{\mathcal{O}\left( l^{1/3} \cdot (\log l)^{2/3}\right)}

  • For a fixed security level, say 2^{128} operations, n and l should be chosen as small as possible

Elliptic Curves

  • A source of prime-order groups where DL is hard
  • More efficient than other groups at any given level of security

Elliptic Curves over Reals

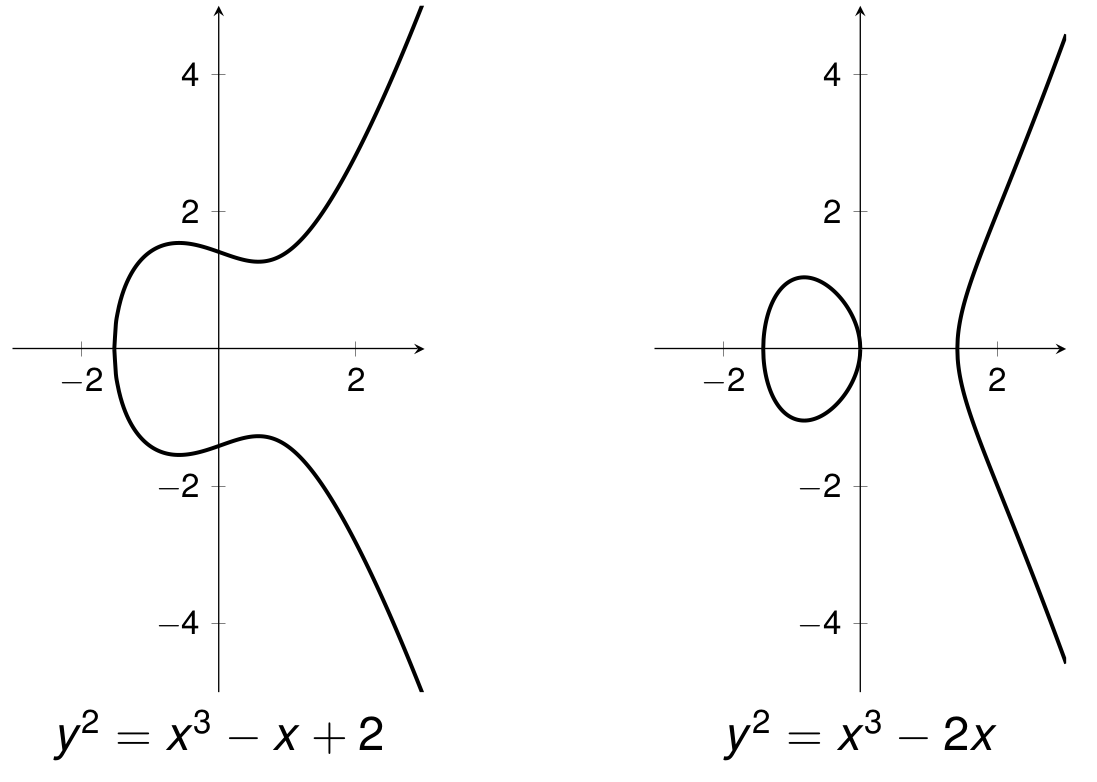
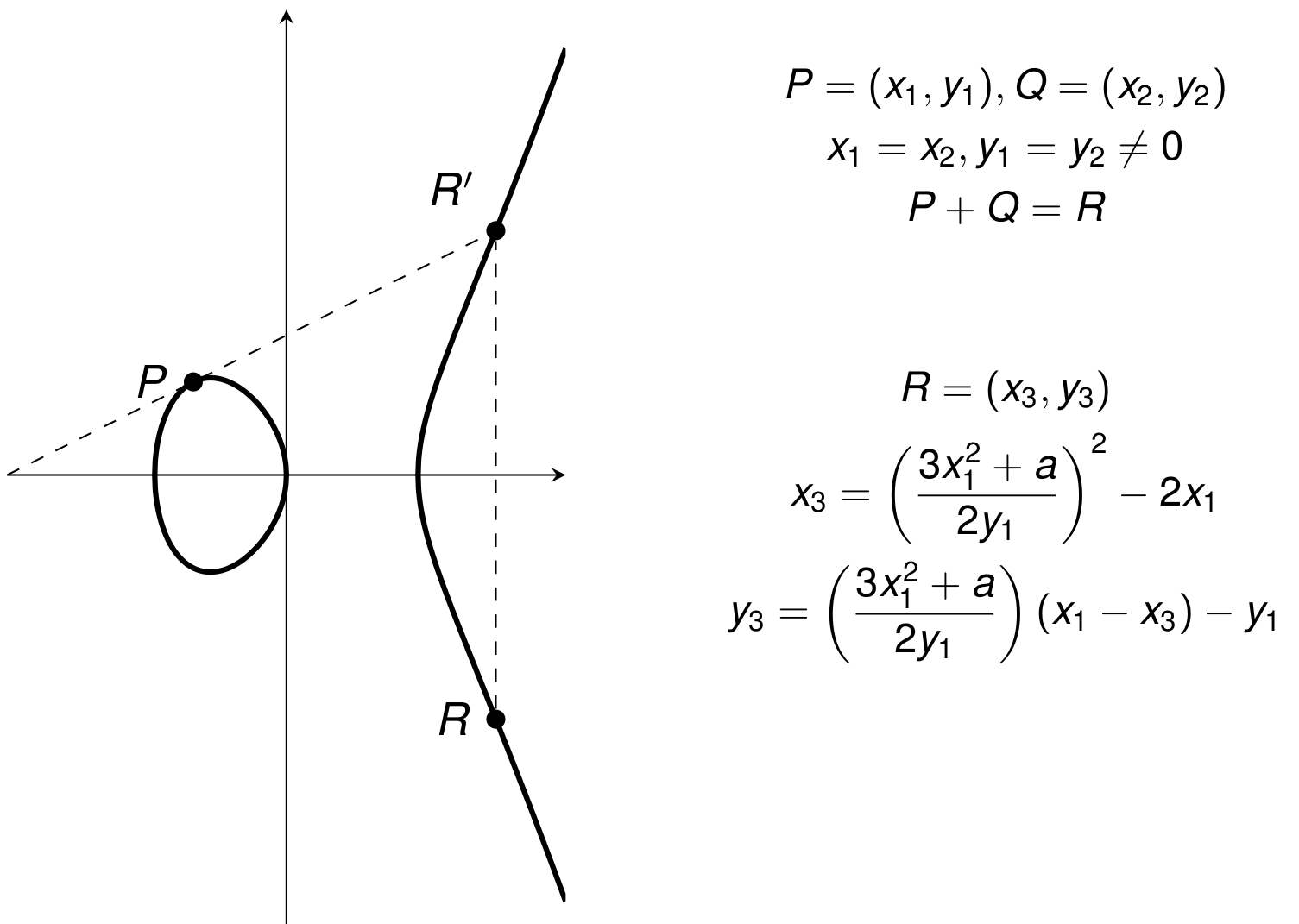
  • The set E of real solutions (x,y) of \begin{equation*} y^2 = x^3 + ax + b \end{equation*} along with a “point at infinity” \mathcal{O} where 4a^3 + 27b^2 \neq 0

  • Weierstrass representation of an elliptic curve

  • Elliptic curves form a group under point addition

Elliptic Curve Examples

Point Addition (1/3)

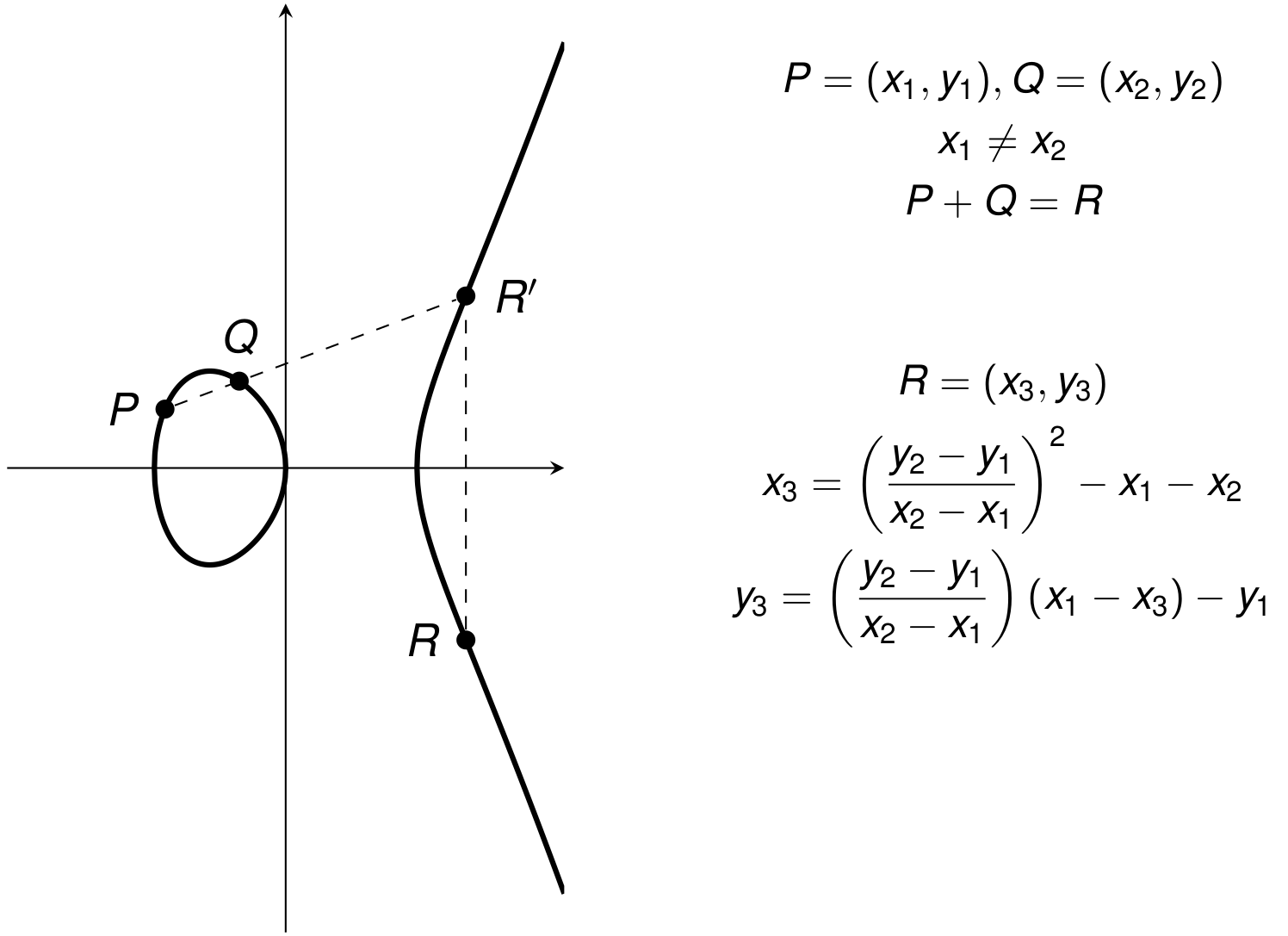
Point Addition (2/3)

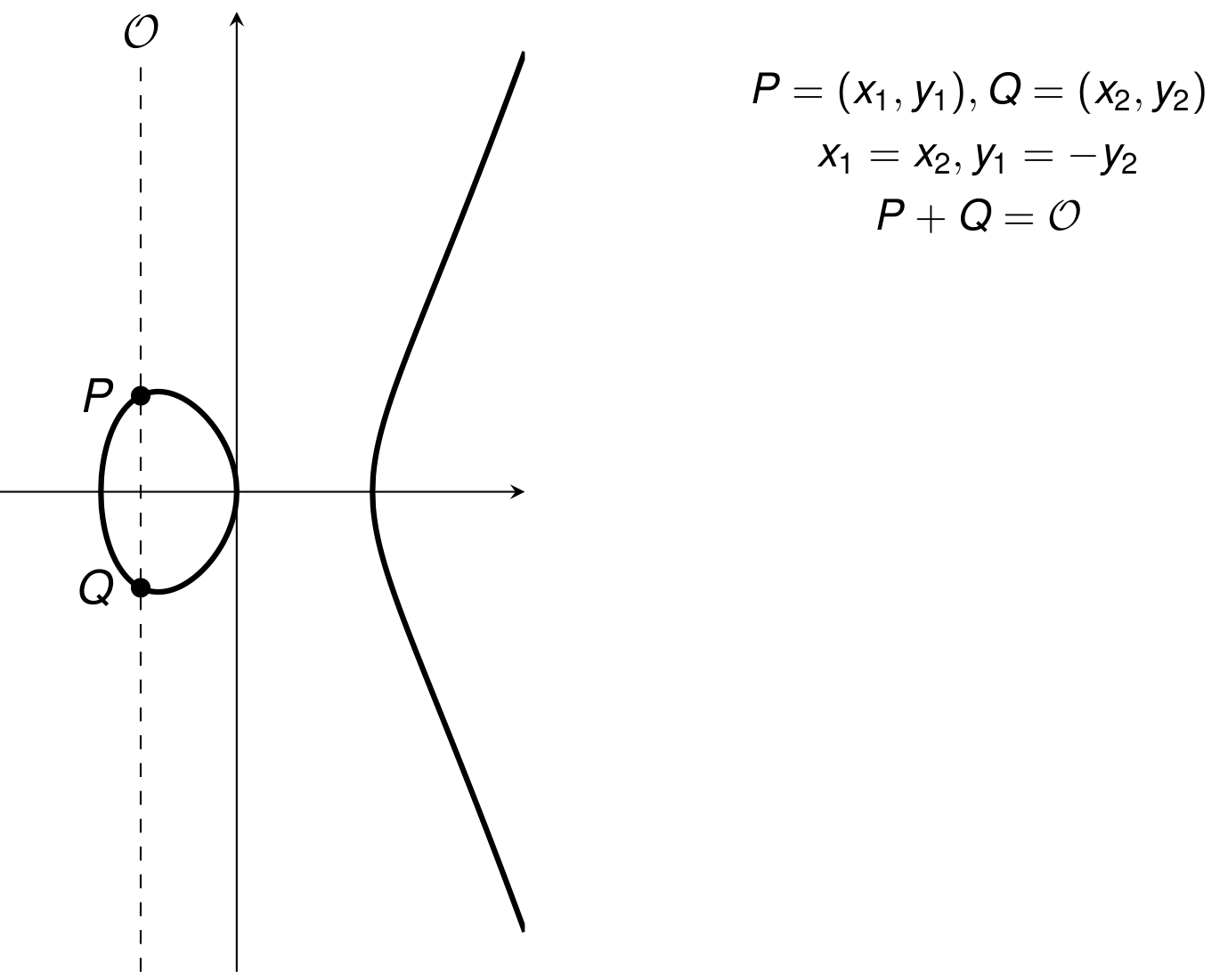
Point Addition (3/3)

Finite Fields

  • A set F together with two binary operations + and \ast is a field if

    • F is an abelian group under + whose identity is called 0
    • F^* = F \setminus \{0\} is an abelian group under \ast whose identity is called 1
    • For any a,b,c \in F \begin{equation*} a \ast (b + c) = a \ast b + a \ast c \end{equation*}

  • A finite field is a field with a finite cardinality.

  • \mathbb{Z}_p is a finite field for prime p

Elliptic Curves over \mathbb{Z}_p

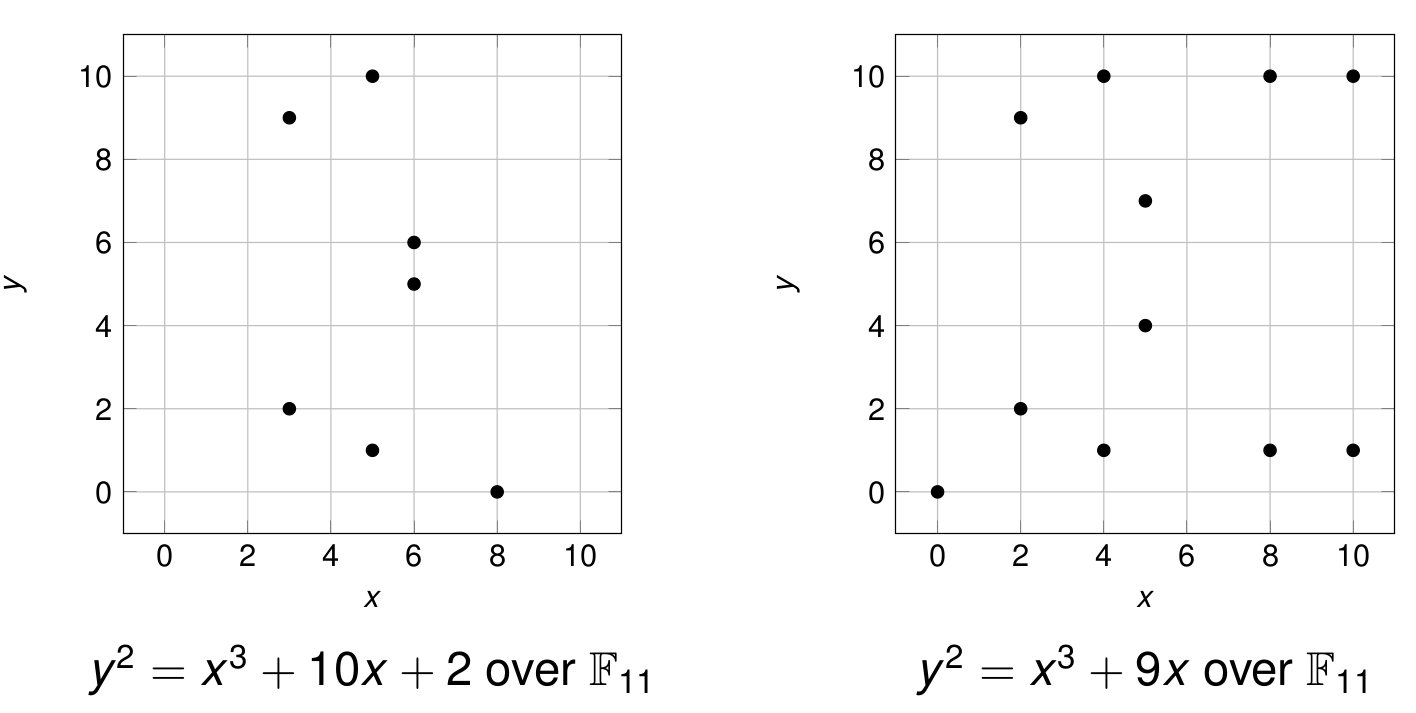
  • For p \ge 5, the set of solutions (x,y) in \mathbb{Z}_p^2 of \begin{equation*} y^2 = x^3 + ax + b \end{equation*} along with a “point at infinity” \mathcal{O} where 4a^3 + 27b^2 \neq 0

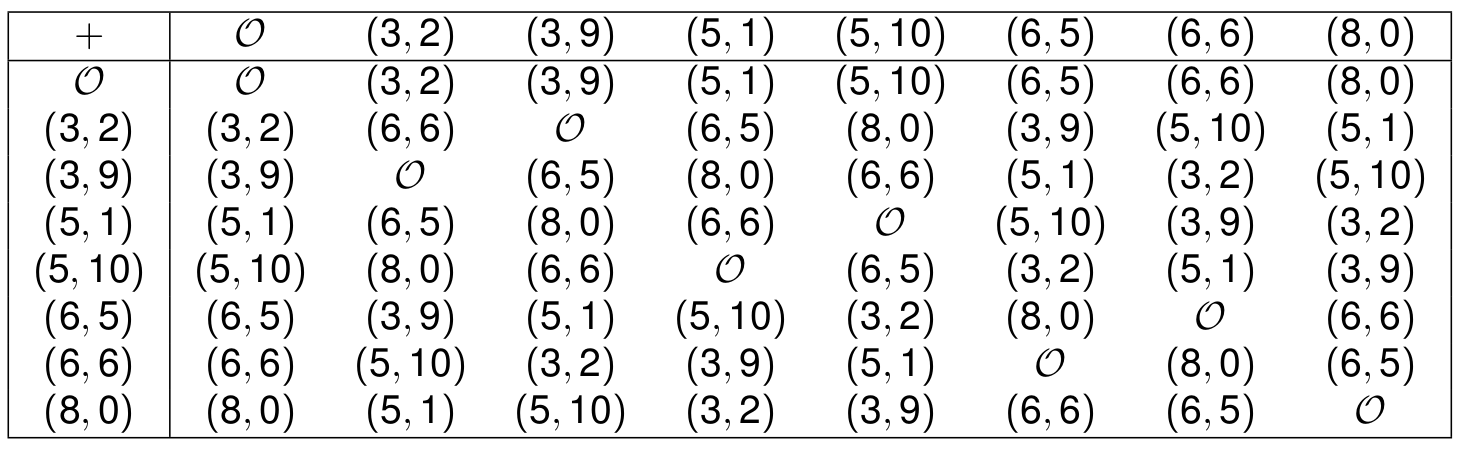
Point Addition for Finite Field Curves

  • Point addition formulas derived from the reals are used

  • Example: y^2 = x^3+10x+2 over \mathbb{F}_{11}

Finding Elliptic Curve Groups of Prime Order

  • There is a polynomial-time algorithm for counting the number of points on an elliptic curve over \mathbb{Z}_p

  • Choose values for a,b in the equations y^2 = x^3 + ax+b and check if |E| is prime or r times a prime

  • In the latter case, choose G = \{rP \mid P \in E\}

Further reading