Nova Aadhaar

Saravanan Vijayakumaran

EE Department, IIT Bombay

March 10, 2025

Age Proofs

  • Cryptographic proofs that a government-issued digital ID contains a birth date of someone who is above a certain age

  • Applications

    • Prove that someone is an adult so that they can access age-restricted resources online
    • Prove that someone is a senior citizen so that they can get special privileges

  • Why not use the ID itself as a proof?

    • Privacy

Aadhaar QR Code

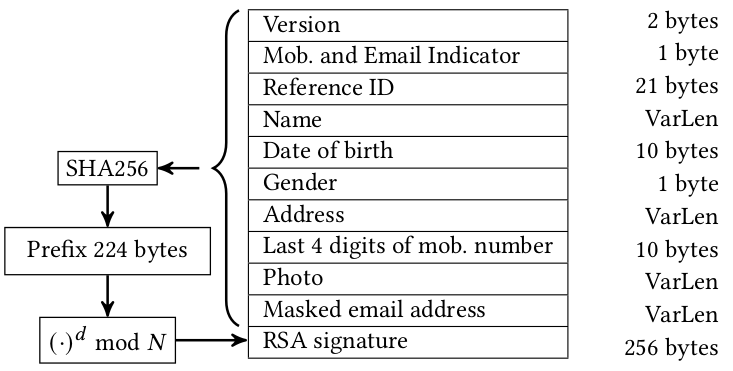
  • Every Aadhaar card contains a QR code that encodes the holder’s personal details including date of birth

  • It also contains an RSA signature created using UIDAI’s private key

  • One can generate an age proof using the Aadhaar QR code

Anon Aadhaar

  • An implementation of an Aadhaar-based age proof by Ethereum Foundation

  • Generates a zero-knowledge (ZK) proof that the Aadhaar QR code contains the birth date of an adult

  • Proofs can be verified on-chain, i.e. in an Ethereum smart contract

  • Uses the Groth16 proof system

  • Main drawback: Resource intensive; needs 600MB/300MB initial download and 1.4 GB/9.6 GB RAM in phone/browser

Our contribution

Android App

Nova

  • A zkSNARK for statements with IVC structure

    • zkSNARK: ZK Succinct Non-interactive ARgument of Knowledge
    • IVC: Incrementally Verifiable Computation

  • Incremental Computation

Incrementally Verifiable Computation

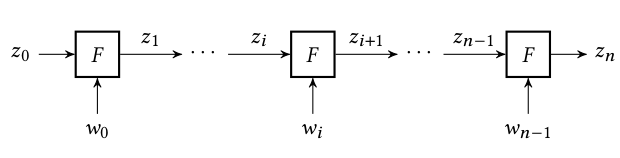
  • An IVC instance is given by \left(F, n, z_0, z_n\right)

  • An IVC scheme allows a prover to prove that

    • for some public step F,

    • public initial input z_0, public final output z_n,

    • it knows auxiliary input values w_0, w_1,\ldots,w_{n-1} such that

      z_n = F \left(\ldots F \left(F \left( z_0, w_0 \right), w_1 \right) \ldots,w_{n-1}\right).

Aadhaar QR Code Data

Age Proof Desiderata

  • Setting: An adult Aadhaar holder will generate and submit an age proof to an application that has a unique AppID

  • Desirable properties

    • Soundness: Only adult Aadhaar holders should be able to generate a valid age proof
    • Privacy: The age proof should not reveal any information about the fields in the Aadhaar QR code, apart from the fact that the holder is an adult
    • Intra-application linkability: An application should be able to link multiple age proofs created by the same Aadhaar holder
    • Inter-application unlinkability: Age proofs generated by the same holder for different applications should not be linkable
    • Low computational requirements: Users should be able to generate the proofs on low-end devices

Strawman Design 1

  • Use the Aadhaar QR code itself as the age proof

  • To verify the age proof, the verifier will

    • first check that the RSA signature is valid using the Aadhaar public key,
    • and then check that the birth date is 18 or more years in the past

  • Satisfies all desiderata except privacy

Strawman Design 2

  • Let \texttt{H} be the SHA256 hash of the QR code data except for the last 256 bytes
  • Let \textsf{sig} be the RSA signature
  • An adult Aadhaar holder could generate an age proof as the triple \left( \texttt{H}, \textsf{sig}, \pi \right) where
    • \pi is a ZK proof that \texttt{H} is the SHA256 hash of some Aadhaar QR code data (excluding RSA signature) and
    • this data contains a date of birth which is 18 or more years in the past
  • The verifier performs the following checks.
    • It first verifies that \textsf{sig} is a valid RSA signature on \texttt{H} using the Aadhaar public key
    • It then verifies that the ZK proof \pi is valid for the instance \texttt{H}
  • This design does not satisfy intra/inter application linkability/unlinkability requirements

Issues with Strawman Design 2

  • Intra-application linkability
    • The SHA256 hash \texttt{H} changes with every download of the QR code since the timestamp changes
    • An adult Aadhaar holder can use two of his QR codes with different timestamps to generate two age proofs having different values for \texttt{H}
  • Inter-application unlinkability
    • The age proof is independent of the AppID
    • Either the hash \texttt{H} or the RSA signature \textsf{sig} can be used to link the age proofs submitted by the same Aadhaar holder to different applications

Nova Aadhaar Statement

  • Let \texttt{qr} be an n-byte array representing the QR code data

  • Let \texttt{qr}_{\text{d}} be the byte array of length n-256 corresponding to \texttt{qr}[0:n-256]

  • Let \texttt{qr}_{\text{m}} correspond to the bytes in \texttt{qr}_{\text{d}} with the 17 timestamp bytes replaced with zero bytes

  • Let \texttt{A}_{\text{id}} be the AppID of the target application for the age proof

  • Let \texttt{H}_{\text{pos}} denote the Poseidon hash function

  • An adult Aadhaar holder will generate an age proof as \left( \texttt{A}_{\text{id}}, \sigma, \pi \right) where \pi is a ZK proof attesting to the following claims:

    • \sigma= \texttt{H}_{\text{pos}}\left(\texttt{A}_{\text{id}}, \texttt{qr}_{\text{m}}\right) for some byte array \texttt{qr}_{\text{m}}. \sigma is called the nullifier
    • There exists a byte array \texttt{qr}_{\text{d}} that agrees with \texttt{qr}_{\text{m}}, except that it has zeroes in the 17 timestamp byte locations
    • The SHA256 hash of the byte array \texttt{qr}_{\text{d}} is \texttt{H}.
    • The prover knows an RSA signature \textsf{sig} on \texttt{H}
    • The date of birth in \texttt{qr}_{\text{m}} is 18 or more years in the past.

How to express the Nova Aadhaar statement as an IVC instance?

  • An IVC instance is given by \left(F, n, z_0, z_n\right)
  • How can we break the Nova Aadhaar statement into steps?
  • What should be the step function F?
  • How many steps n?
  • What should the values of z_0, z_n be?

First Key Insight

  • The SHA256 hash function already has an incremental structure

  • The SHA256 hash of a bitstring M \in \{0,1\}^* is calculated as follows.

    • The bitstring M is padded to a multiple of 512 bits to obtain M_{\text{padded}}.
    • A 256-bit state variable H^{(0)} is initialized using bits from the square roots of the first eight primes.
    • M_{\text{padded}} is split into N blocks M^{(1)}, M^{(2)},\ldots,M^{(N)} each having 512 bits (64 bytes).
    • Using a compression function f: \{0,1\}^{512} \times \{0,1\}^{256} \to \{0,1\}^{256}, the values of H^{(i)} are calculated as H^{(i)} = f\left( M^{(i)}, H^{(i-1)} \right), for i=1,2,\ldots,N
    • The 256-bit string H^{(N)} is the SHA256 hash of M.

Second Key Insight

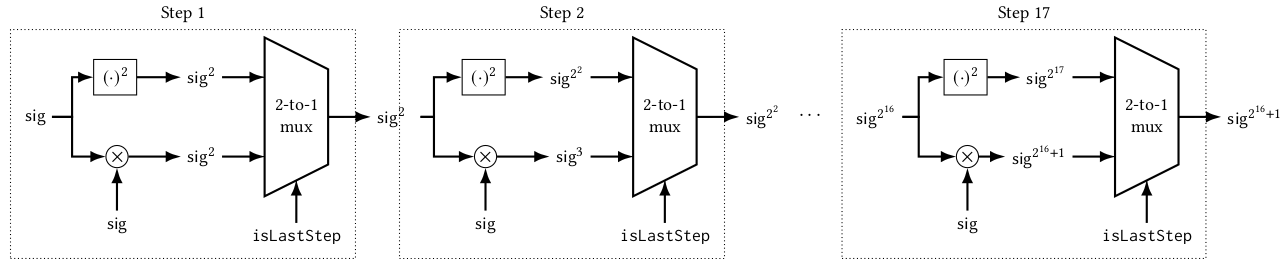
  • The RSA exponent e in the Aadhaar public key has the value 65537 = 2^{16}+1

  • The exponentiation \textsf{sig}^e can be spread over 17 steps where

    • the first 16 steps perform a squaring operation and
    • the last step performs a multiplication

  • Since F has to be the same in every step, we can use a multiplexer to choose between the outputs of the squaring operation and product operations

Splitting the QR code data

  • The step function F has to check the DoB
  • The DoB field appears after the variable-length Name field
    • It could lie in the first 64-byte block, in the second 64-byte block, or span the boundary between the blocks
  • To simplify F, we hash two 64-byte blocks in each step

Nullifier Calculation

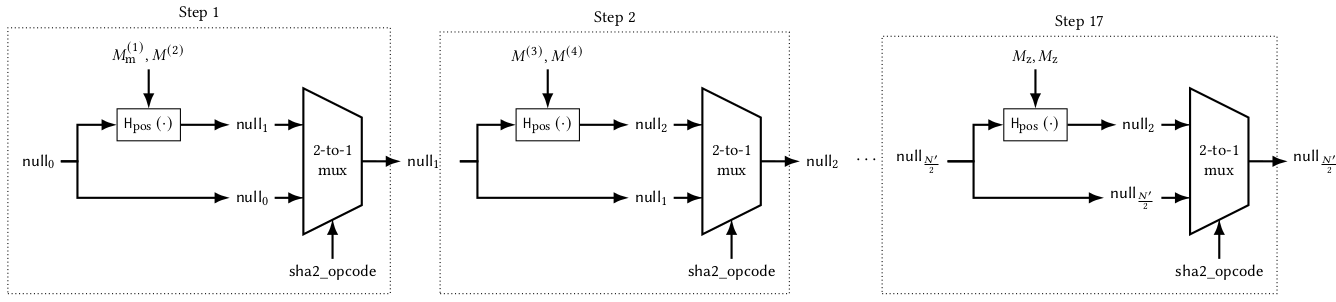
  • Recall that the nullifier is \sigma= \texttt{H}_{\text{pos}}\left(\texttt{A}_{\text{id}}, \texttt{qr}_{\text{m}}\right)
  • We set \textsf{null}_0 = \texttt{A}_\text{id}
  • As long as SHA256 hashing is active, we recursively hash the previous nullifier value to get the new one

Public Inputs/Outputs

  • Initial inputs \begin{align*} z_0 = \begin{bmatrix} \textsf{initial\_opcode} & \textsf{current\_date} \end{bmatrix}, \end{align*}
  • Final inputs \begin{align*} z_n = \begin{bmatrix} \textsf{final\_opcode} & \textsf{final\_nullifier} \end{bmatrix}, \end{align*}
  • The opcodes control the decisions at each step

Step Function F

Please see preprint for full specification

Performance

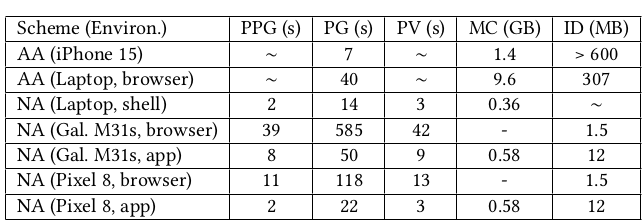
  • AA = Anon Aadhaar, NA = Nova Aadhaar
  • PPG = Public parameter generation, PG = Proof Generation, PV = Proof Verification
  • MC = Peak Memory Consumption, ID = Initial Download

Code repositories

Thanks for listening

URL of Nova Aadhaar preprint