Research!
My area of work in PhD is
tracking. This is an active area in
Computer Vision and has been so for a long time. This is because the
task is tracking consists of many sub-problems and approaches. Also,
people more or less agree that there is no "silver bullet" tracker
which will perform well in all scenarios. The idea is to design a
tracker for a particular scenario. An excellent recent review of
tracking is by Yilmaz et al.
Regarding implementation, I have used OpenCV for all my coding. This is a very stable
library, gaining rapidly in popularity. It can be downloaded
from the Sourceforge site.If need be, I can share the code; feel
free to contact me if you think the code could be useful for you.
Keeping this in mind, our
approach is to use contours for
tracking. The advantage is that the obtained silhouette is a very good
descriptor for activity analysis applications. For implementing the
contours, we used the B Splines; the advantages being speed and ease of
implementation. Compared to the level set framework, the
disadvantage is that topology change is not possible without special
and cumbersome procedure. We however assume that topology change does
not occur for our applications; we do not expect a person to split into
two! Our first work is on stabilisation of active contours, as
described next.
Note that all copyrights rest with the respective publishers.
Stabilisation of Parametric Active Contours
Parametric contours have
an interesting implementation
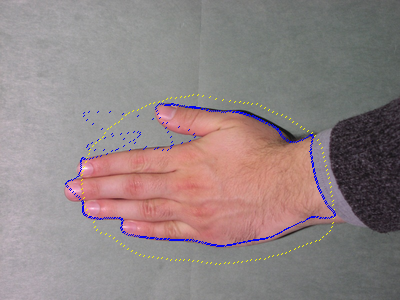
problem. This is best observed in the image below left. The image shows
the
segmentation of the hand using the region based active contour model of
Zhu and Yuille. The yellow curve is the initialisation and the blue
cuve shows the final curve. The segmentation has is not good because
of the looping of the contour.
other parts. For B Splines, this
bunching of points leads to formation of loops, because the control
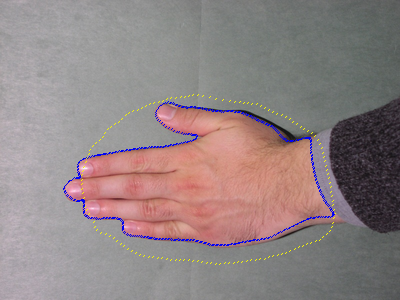
points also come closer together. We have proposed an ODE to
control the spacing of the the curve points. This stabilises the curve,
in the sense that the uniform spacing between the curve points is
maintined throughout the evolution. This ODE determines the tangential
component of the curve evolution, and it has been shown that the
proposed tangential term is bounded and hence numerically stable. Using
the proposed tangential term, we get the following segmentation shown
on the right.
Publications:
1. V. Srikrishnan, S. Chaudhuri and S. Dutta Roy, "Stabilisation of Active Contours
Using Tangential Evolution Term: An application to Tracking",
Proc. ICCTA, Kolkata, March 2007.
2. V. Srikrishnan, S. Chaudhuri, S. Dutta Roy and D. Sevcovic,
"On Stabilisation of
Parametric
Active Contours", Proc. CVPR, Minneapolis, June
2007.
3. V. Srikrishnan, S.Chaudhuri "Stable contour tracking through
Tangential Evolution", Book chapter in Advances in Intelligent
Information Processing:Tools and Applications, Eds. B. Chanda and C. A.
Murthy, World Scientific, 2008.
4. V. Srikrishnan, S. Chaudhuri, "Stabilisation of Parametric Active
Contours using a Tangential Redistribution Term", IEEE Trans. Image
Processing(accepted).
Extension to Open Curves
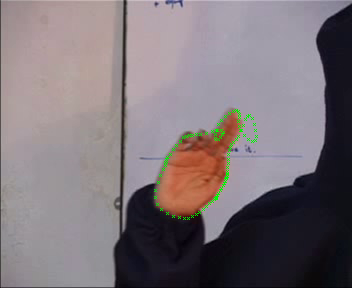
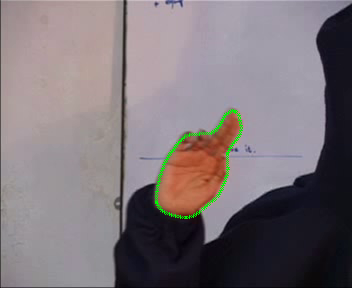
We have applied our technique for evolution of open curves also. We used the active contour model proposed by Kimmel and Bruckstein. The results are as below

The line in pink/red is the initialisation. The yellow line shows the curve after some amount of evolution. The image at the bottom shows the final result.
Videos
Here is video which show the failure without the tangential reparametrisation. For the same sequence, we show the stabilised contour evolution here. All videos were encoded using mencoder, these may not play in Windows media player. Some other sequences are Daria, Ido-bend, Ido, Ira-bend and Balloon sequences.Salient Contours
Energy minimising functionals for contours can be region or gradient based. In the gradient based framework, the contours are generally attracted towards the nearest strong edges. One of the most popular techniques is the Gradient Vector Force(GVF) snake. This model has however a typical problem of getting attracted to the "wrong" edges, because of poor initialisation or due to a strong edge overwhelming a weak one. In this work, we try to overcome this major drawback and propose a model which has much more interesting property. The results are as shown below.

The curve in red shows the initialisation and the curve in green shows the final segmentation. Note that these implementations use the tangential stabilisation introduced earlier. Here are some more results. The image on the left is using the standard GVF model, the image on the right is the result using our technique. Here are two more results, as usual, the one on the left benig obtained from the standard GVF method and the one on the right using the proposed method.
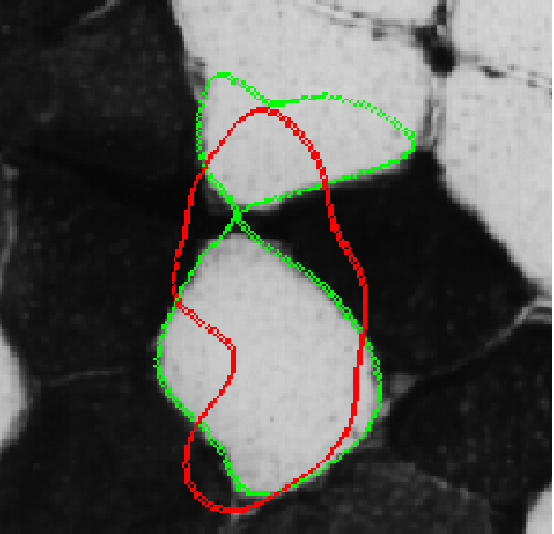
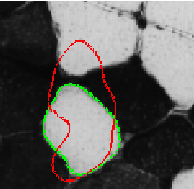
The basic idea behind the work is that object outlines in the real
world are continuous but may consist of strong and weak edges. This is
a common observation. Given the fact that there generally are many
strong edges near the object of interest, it is not surprising that
most gradient based techniques fail in delineating the correct and
complete object outline despite apparent increase in
sophistication of the model. We use a curve varying internal energy
term to pull back the curve segments to the correct edge.
Videos ( Updated )
We have applied our technique of real life videos from the Caviar
database. 1. OneStopNoEnter2cor sequence: GVF method, our method.
2. ShopAssistant1cor sequence: GVF method, proposed approach.
Publications:
1. "Distraction-Free Evolution of Active Contours", Proc. 7th Intl. Conf. on Advances in Pattern Recognition (ICAPR), Kolkata, 2009. pdf
Combination of Mean Shift and Contour based tracker
As is well known, the mean shift tracker is very fast. It has three major problems, firstly that no shape information is generated. More importantly, the base mean shift tracker does not encode appearance information well. Finally, the bandwidth problem is well known in literature, that is, how do we set the size and orientation of the bounding ellipse?On the other hand, the contour based tracker is very slow. Therefore, we try to utilise the benefits of each tracker to overcome the disadvantage of the other. We use the mean shift approach to move the contour for translational motion. Then, in the new position the contour evolution proceeds as per the energy functional. This final convergence of the contour provides the initialisation of the mean shift for the next frame.
Publication:
1. V. Srikrishnan and S. Chaudhuri, ``Kernel Snake: A Cooperative Shape Tracking Paradigm", Proc. National Conf. Communication (NCC), IIT Mumbai, India, Jan 2008. (pdf)
Fragment based tracking for Scale and Orientation adaptation
In this work, we propose a simple yet highly effective approach to handle the scale and orientation problem in blob based tracking approached. Fragment based tracking has been used in literature to tackle the problem of tracking through partial occlusion, where the non occluded portion is used to maintain track. We have experimented with several challenging real life videos: Anup, Book, Satya-increase, Satya-decrease, PETS1 and PETS2 sequences.Publication
1. V. Srikrishnan, T.N.P Nagaraj and S. Chaudhuri, "Fragment based tracking for Scale and Orientation adaptation", Proc. ICVGIP, Bhubaneswar, India, December 2008.(accepted) pdf
© 2007 V. Srikrishnan | Design by Andreas Viklund